Справочная информация

РЕШЕНИЕ СИСТЕМ НЕЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ

0.1337 0.2099 -0.2491 0.1949

-0.3556 -0.1793 0.5064 0.0043

0.3353 -0.2280 -0.4126 -0.4403

0.0620 0.5372 0.1037 0.4815

-0.4893 -0.2886 0.0231 -0.1906

0.4893 -0.2886 0.0231 0.1906

-0.0620 0.5372 0.1037 -0.4815

-0.3353 -0.2280 -0.4126 0.4403

0.3556 -0.1793 0.5064 -0.0043

-0.1337 0.2099 -0.2491 -0.1949

Собственные векторы - первые 4

3.188 3.206 3.591 3.784

Собственные значения - первые 4

Контрольные задания

Решить задачу на собственные значения, найдя не менее 4-х наименьших по модулю собственных значений и соответствующих им собственных векторов. Сделать проверку для найденных собственных векторов и собственных значений, подставив их в исходную систему линейных алгебраических уравнений. Систему уравнений взять по номеру своего варианта, заменяя им переменную n.

1–5.
6–10.
11–15.

16–20.
21–25.
26–30.

Система нелинейных алгебраических уравнений относительно неизвестных x ₁, x ₂,..., x_n записывается в общем виде следующим образом

или в матричной форме

,

где

.

Методы решения таких систем делятся на три основные группы: методы уточнения начального приближения решения, методы продолжения решения и поисковые алгоритмы, предназначенные для отыскания экстремума функции многих переменных, эквивалентной исходной системе нелинейных алгебраических уравнений.

Метод Ньютона–Рафсона

Данный метод относится к методам последовательного уточнения первоначального приближения решения. Каждое его новое приближение к значению вектора решения системы уравнений f (x) = 0 ищется по следующей итерационной схеме

,

,

…………………………

,

………………….………

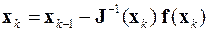где x ₀ – первоначальное приближенное значение вектора решения системы, а J (x) – матрица Якоби системы уравнений, состоящая из производных левых частей уравнений системы

.

Здесь, при записи матрицы Якоби использовано сокращённое обозначение частных производных

.

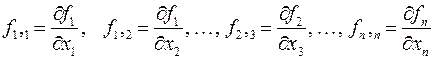Выполнение каждой итерации за счёт того, что в ней присутствует обратная матрица J ^–1(x), идентично решению системы линейных алгебраических уравнений

,

из которой по известному вектору x _{k –1} находится вектор следующего приближения решения x _k

.

В развернутой форме k -я итерация записывается следующим образом

, .

Если во всех точках n -мерной области , в которой лежит вектор точного решения x _т и его приближения x ₀, x ₁,..., x _k,..., все составляющие векторной функции f (x) имеют непрерывные первые и вторые производные

и

со следующими оценками норм

,

для которых выполняется условие

,

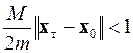то итерационный процесс метода Ньютона–Рафсона сходится к точному решению системы x _т для любого начального приближения x ₀, взятого из области .

В этом случае абсолютная погрешность вектора приближённого решения на k -ой итерации определяется соотношением

.

На практике пользуются более грубой оценкой абсолютной погрешности. Если итерации метода Ньютона–Рафсона сходятся к точному решению системы x _т, то абсолютная погрешность вектора приближённого решения на k -ой итерации можно оценить неравенством

.

Алгоритм метода Ньютона–Рафсона может быть проиллюстрирован на примере решения следующей системы уравнений

На первом этапе записывается матрица Якоби решаемой системы

,

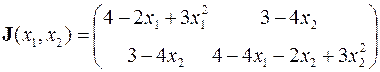с помощью которой формируется итерационная схема метода Ньютона–Рафсона

,

где

На втором этапе с помощью полученной итерационной схемы последовательно выполняются операции получения приближённого решения системы. Для этого в качестве начального приближения вектора решения берётся нулевой вектор

Первая итерация:

- формирование матрицы Якоби системы уравнений

,

- вычисление левых частей системы уравнений

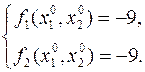
- формирование системы линейных уравнений для поправок

,

- решение системы линейных уравнений

- получение первого приближения вектора решения

Вторая итерация:

- формирование матрицы Якоби системы уравнений

,

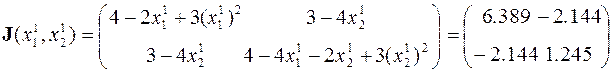- вычисление левых частей системы уравнений

- формирование системы линейных уравнений для поправок

,

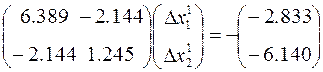- решение системы линейных уравнений методом Гаусса

- получение второго приближения вектора решения

Далее процесс уточнения вектора решения исходной системы нелинейных уравнений продолжается. На 9-й и 10-й итерациях приближённое решение имеет следующие составляющие

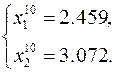
Оценка абсолютной погрешности 10-го приближения решения может быть получена по следующей формуле

.

а относительной погрешности – следующим образом

.

Проверка полученного решения с помощью исходных уравнений даёт следующие значения для их левых частей

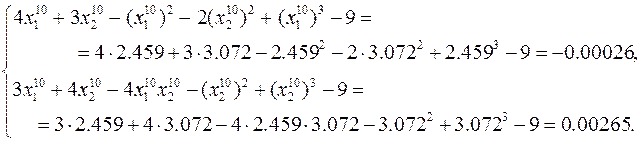
Метод непрерывного продолжения (Д.Ф.Давиденко, 1953)

Появление методов продолжения было вызвано необходимостью решения систем нелинейных алгебраических уравнений большого порядка, когда метод Ньютона–Рафсона и ему подобные либо дают приемлемый по точности результат за очень большое количество итераций, либо, что случается чаще, вообще расходятся.

Метод непрерывного продолжения основан на введении в систему алгебраических уравнений

f (x) = 0

некоторого параметра t – параметра продолжения

g (x, t) = 0,

при одном значении которого решение новой системы известно

g (x, t ₀) = 0: x = x ₀,

а при другом его значении t_m её решение совпадает с решением исходной системы

g (x, t_m) = 0: x = x _m x _т.

Например, дана система уравнений

Она может быть преобразована как

Эта система при t ₀ = 0 имеет точное решение , а при t_m = 1 её решение совпадает с решением исходной системы.

Система нелинейных алгебраических уравнений с параметром t в методе непрерывного продолжения рассматривается как описание в неявной форме решения задачи Коши с начальным условием x (t ₀) = x ₀ для векторной переменной x (t). Система обыкновенных дифференциальных уравнений для этой задачи Коши – система уравнений продолжения, получается дифференцированием уравнений полученной системы алгебраических уравнений по параметру t

,

где

,

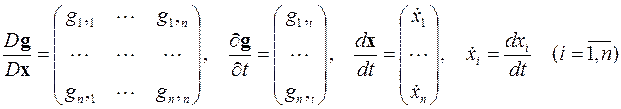а производная Фреше D g / D x, являющаяся квадратной матрицей, называется ещё матрицей Якоби J системы нелинейных алгебраических уравнений.

Полученная таким способом задача Коши для уравнений продолжения

,

которая в развёрнутом виде записывается следующим образом

решается одним из известных методов до значения аргумента, равного t_m, при котором системы алгебраических уравнений g (x, t) = 0 и f (x) = 0 совпадают. Значение вектора x в точке t_m будет являться приближением решения x _т исходной системы.

Используемая постановка задачи Коши содержит систему дифференциальных уравнений, неразрешённых относительно производных, в то время как методы её численного решения (метод Эйлера, методы Рунге–Кутта и другие) применимы только для нормальных систем вида

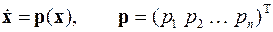
или

Поэтому на каждом шаге этих методов для вычисления вектора правых частей нормальной системы дифференциальных уравнений необходимо решать следующую систему линейных алгебраических уравнений

,

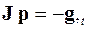что может быть выполнено методами Гаусса, простых итераций, Зейделя или любым другим.

Получающееся решение x (t) рассматриваемой системы уравнений описывает некоторую кривую в (n + 1)-мерном пространстве, образованном составляющими вектора решения системы 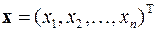и параметром t, который выполняет в данном случае роль аргумента. По традиции, пришедшей из механики деформируемого твёрдого тела, эта кривая называется траекторией нагружения или траекторией решений.

Погрешность получаемого таким способом решения исходной системы нелинейных алгебраических уравнений определяется двумя процессами. Первый из них – метод решения системы линейных алгебраических уравнений, определяющей вектор правых частей нормальной системы дифференциальных уравнений, а второй – метод решения задачи Коши для этой системы. Оценки погрешностей решений, которые они дают по отдельности, известны (см. [3], разделы 3 и 7). Однако в случае их совместного многократного применения получить объединённую оценку погрешности решения, получаемого при t = t_m затруднительно. Выходом из такой ситуации может служить использование любого метода решения систем нелинейных алгебраических уравнений, в частности, метода Ньютона–Рафсона.

При этом алгоритм решения задачи будет строиться по следующей схеме. Сначала исходная система нелинейных алгебраических уравнений решается методом непрерывного продолжения от t ₀ до t_m и получается её приближённое решение, а потом оно используется как начальное приближение для метода Ньютона–Рафсона, с помощью которого оно уточняется до необходимой степени. Погрешность такого решения будет определяться погрешностью, даваемой методом Ньютона–Рафсона, и оценить её можно по его известным соотношениям.

В качестве примера применения метода непрерывного продолжения можно рассмотреть задачу о решении системы уравнений

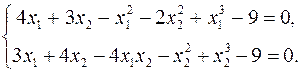
На первом этапе она приводится к виду, необходимому для применения метода непрерывного продолжения

Далее полученная система дифференцируется по параметру t, что даёт систему уравнений продолжения, являющуюся системой обыкновенных дифференциальных уравнений, не разрешённых относительно производных

Отрезок изменения параметра t от 0 до 1 разбивается на 5 частей с шагом h = 0.2 и с помощью метода Эйлера организуется процесс продолжения по выбранному параметру. Причём на каждом шаге метода Эйлера, который применим для решения задачи Коши вида

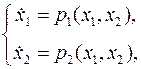
для определения значений функций p ₁(x ₁, x ₂) и p ₂(x ₁, x ₂) должна решаться система линейных алгебраических уравнений

Второй этап решения заключается в применении метода Эйлера:

t ₀ = 0: ® ®

t ₁ = 0.2: ®

® ®

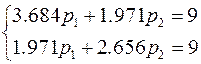t ₂ = 0.4: ®

® ®

t ₃ = 0.6: ®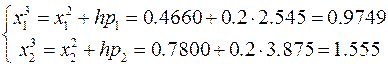

® ®

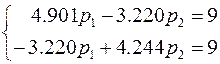t ₄ = 0.8: ®

® ®

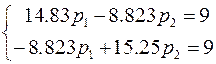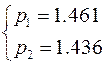
t ₅ = 1.0:

На третьем этапе полученное решение уточняется методом Ньютона–Рафсона, для чего в качестве начального приближения берутся значения

Две итерации метода Ньютона–Рафсона дают следующие приближения

и

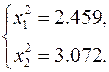
Погрешность этого решения определяется аналогично предыдущему решению рассматриваемой системы нелинейных алгебраических уравнений

ε _абс £ 0.014, ε _отн £ 0.46%.

Оптимизация параметра продолжения

Нелинейные задачи, включая задачу решения систем нелинейных алгебраических уравнений, являются одними из самых коварных задач вычислительной математики. Такая их характеристика обусловлена в первую очередь не единственностью их решения. Из-за этого методы типа метода Ньютона–Рафсона и поисковые алгоритмы либо расходятся, либо позволяют находить только одно решение из нескольких, а применение методов продолжения часто приводит к аварийному останову ЭВМ из-за переполнения разрядной сетки. Последнее явление обусловлено наличием на траектории решений x (t) особых точек. К ним относятся предельные точки, точки бифуркации, точки возврата и др. Пример траектории решений с простейшими особыми точками – четырьмя предельными точками, которые отмечены кружочками, показан на рис.1.

Рис.1.

В особых точках матрица Якоби системы нелинейных алгебраических уравнений вырождается, решение системы линейных алгебраических уравнений с ней становится невозможно и, как следствие этого, становится невозможным продолжение решения через них. Выходом из такой ситуации является использование идеи равноправия аргументов системы нелинейных алгебраических уравнений (E.Riks, 1972), в соответствии с которой ранее введённый параметр продолжения t считается такой же независимой переменной, как все остальные x ₁,…, x_n

t = x_{n +1}.

В этом случае система из n нелинейных алгебраических уравнений с n аргументами и параметром t становится недоопределённой. Она, как и ранее, состоит из n уравнений, но количество неизвестных в ней становиться равным n +1

,

где

.

Аналогичная ситуация наблюдается и с уравнениями продолжения решения, которые записываются следующим образом

,

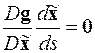где

.

Однако это обстоятельство предоставляет широкие возможности для выбора нового параметра продолжения s. Его можно выбрать наилучшим образом с той точки зрения, чтобы матрица Якоби получающихся уравнений продолжения не вырождалась бы в предельных точках траектории решений.

Как показали исследования, таким параметром является длина дуги траектории решений, связанная с аргументами x ₁,…, x_n, x_{n +1} известным образом

.

Это соотношение, связывающее параметр продолжения s с аргументами x ₁,…, x_n, x_{n +1} системы нелинейных алгебраических уравнений, будучи записанным в дифференциальной форме

,

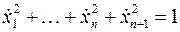однозначно доопределяет уравнения продолжения, приводя их к виду

,

где

,

а матрица называется расширенной и дополненной матрицей Якоби, которая не вырождается в предельных точках траектории решений.

Далее, как было показано ранее, для применения численных методов решения задачи Коши для уравнений продолжения они должны быть приведены к нормальному виду

.

Для этого на каждом шаге этих методов для вычисления вектора правых частей нормальной системы дифференциальных уравнений должна решаться следующая система линейных алгебраических уравнений

.

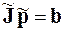Однако последняя строка матрицы , состоящая из компонент вектора продолжения на каждом шаге по траектории решений, неизвестна. Простейшим способом преодоления этого препятствия является их замена на аналогичные компоненты с предыдущего шага

.

При этом для первого шага по траектории решений вектор задаётся в виде единичного вектора

,

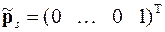причём после вычисления вектора посредством численного решения система линейных алгебраических уравнений для матрицы его надо нормировать.

О вычислении матрицы Якоби

Матрица Якоби, являющаяся производной Фреше – производной от вектора функции по вектору аргументу, представляет собой квадратную матрицу, элементами которой являются частные производные каждой функции по каждому аргументу. Поэтому их аналитическое описание часто бывает затруднительно, а при большом числе уравнений – невозможно. В этом случае прибегают к приближённому вычислению элементов матрицы Якоби.

По определению частная производная i -ой функции g_i (x ₁,…, x_n) по j -му аргументу x_j записывается в виде предела отношения приращения функции к приращению аргумента

.

Это описание производной имеет ещё один вид

.

Отсюда следует возможность приближённого вычисления этой частной производной

,

где h – малая величина, которую часто выбирают в виде 0.1÷0.5 от абсолютной погрешности ε _абс поиска решения исходной системы нелинейных алгебраических уравнений.

Приближённая формула, с помощью которой вычисляется частная производная, называется центральной конечной разностью для первой производной. Она имеет оценку погрешности в виде следующего неравенства

,

где коэффициент C ₂ определяется свойствами функции, чья производная вычисляется таким способом.

Дата добавления: 2014-12-16