Программное обеспечение. В математической библиотеке Matlab’а для решения краевых задач, записанных для нормальных систем обыкновенных дифференциальных уравнений с граничными

В математической библиотеке Matlab’а для решения краевых задач, записанных для нормальных систем обыкновенных дифференциальных уравнений с граничными условиями при x = a и x = b, имеется функция bvp4c. Обращение к ней осуществляется командой

sol=bvp4c(fxy,gru,initsol,opt,P1,P2,...)

В качестве параметров в этой функции используются:

fxy	–	функция, вычисляющая вектор f(x,y) пра­вых частей системы дифференциальных уравнений;
gru	–	функция, определяющая граничные условия при x = a и x = b через описание вектор-функци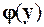й и ;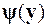
initsol	–	структура с информацией о начальном приближении к вектору решения y(x);
opt	–	структура, задающая параметры вычислительного процесса функции bvp4c. Это необязательный параметр. При его отсутствии функция bvp4c использует настройки по умолчанию, в частности, максимально допустимая относительная погрешность решения принимается равной 10^–3;
P1,P2,...	–	необязательные параметры, которые могут потребоваться для описания вектора пра­вых частей системы дифференциальных уравнений или граничных условий.

Функция fxy, вычисляющая вектор f (x, y) пра­вых частей системы дифференциальных уравнений, должна быть оформлена следующим образом:

function f=fxy(x,y,P1,P2,...)

f(1)=......................;

...........................;

f(n)=......................;

end

Здесь f – массив значений вектора f (x, y) правых частей системы уравнений, x – аргумент x системы уравнений, y – массив значений вектора решения y (x) системы уравнений.

Функция gru, описывающая граничные условия, оформляется в виде:

function g=gru(ya,yb,P1,P2,...)

g(1)=......................;

...........................;

g(n)=......................;

end

Здесь g – выходной массив значений векторов 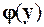(с первого по s-ю компоненту) и 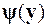(с (s+1)-й по n-ю компоненту) левых и правых граничных условий, ya – массив значений вектора решения y (x) системы уравнений на левом краю при x = a, yb – массив значений вектора решения y (x) на правом краю при x = b.

Структура initsol с информацией о начальном приближении к вектору решения задаётся тремя командами:

xinit=linspace(a,b,m);

yinit=[0;0;...;0];

initsol=bvpinit(xinit,yinit);

Здесь функция linspace формирует одномерный массив-строку xinit координат начальной равномерной сетки на аргументе x в пределах от a до b с шагом интегрирования h = (b – a)/(m –1). Переменная yinit должна быть либо матрицей размера п на m элементов, либо столбцом из п элементов. Компоненты матрицы yinit задают начальные зна­чения вектора решения y (x) краевой задачи в узлах сетки. Если yinit – вектор-столбец из n элементов, то начальные зна­чения вектора решения y (x) считаются одинаковыми для всех узлов начальной равномерной сетки на аргументе x. На основании предварительной информации о начальном приближении решения краевой задачи функция bvpinit генерирует структуру initsol с необходимой информацией для начала работы функции bvp4c построения этого решения с заданной погрешностью.

Структура opt содержит информацию о настройках функции bvp4c. Их перечень функции можно получить с помощью команды bvpset без параметров. Если требуется установить некоторые параметры процесса решения краевой задачи, отличные от тех которые используются по умолчанию, например иную относительную погрешность решения (10^–5 вместо 10^–3) и ограничение по числу узлов сетки на аргументе x (не более 300 узлов), то можно воспользоваться командой

opt=bvpset('reltol',1.0e-5,'Nmax',300);

Результатом обращенияк функции bvp4c являются структура sol, содержащая найденное решение краевой задачи: sol.x – одномерный массив значений аргумента системы дифференциальных уравнений, sol.y – двумерный массив значений вектора решения задачи.

Дата добавления: 2014-12-16