Метод стрельбы

Одним из эффективных методов решения рассматриваемых краевых задач является метод стрельбы, который иногда называют методом пристрелки или методом прогонки. Его идея состоит в сведении краевой задачи к задаче Коши, для которой существуют хорошо отработанные методы численного решения.

На самом деле, краевая задача для нормальной системы дифференциальных уравнений может быть заменена задачей Коши

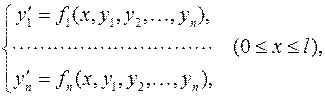
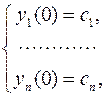
где постоянные с ₁, с ₂,…, с_n подбираются так, чтобы её решение совпадало с решением исходной краевой задачи.

Это достигается следующим способом. Решение задачи Коши кроме аргумента x будет содержать постоянные с ₁, с ₂,…, с_n

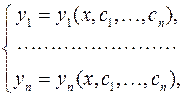
а, следовательно левые части граничных условий в точках x = 0 и точке x = l тоже будут функциями этих постоянных, так как

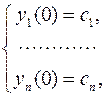
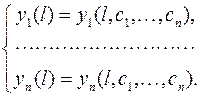
Таким образом формируется система из n алгебраических уравнений относительно n неизвестных с ₁, с ₂,…, с_n

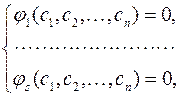
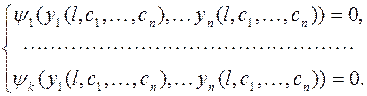
Все сказанное выше позволяет сформировать алгоритм решения линейной краевой задачи методом стрельбы.

Пусть линейная краевая задача записана в общем виде следующим образом:

,

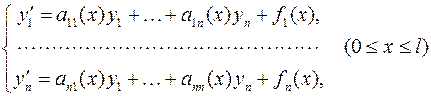при x = 0 при x = l

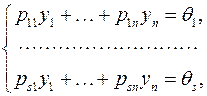
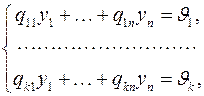
где a ₁₁(x),…, a_nn (x), f ₁(x),…, f_n (x) – ограниченные на отрезке [0, l ] известные функции, а p ₁₁,…, p_n, q ₁₁,…, q_kn, θ ₁,…, θ_s и 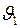,…, 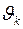– заданные постоянные.

В матричной форме эта краевая задача имеет вид

,

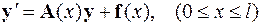при x = 0: 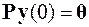, при x = l: ,

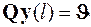где

,

.

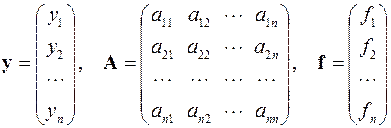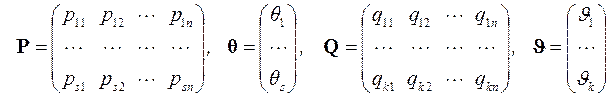Эквивалентная ей задача Коши имеет вид

, ,

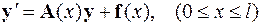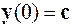где с – вектор, составленный из постоянных с ₁, с ₂,…, с_n

,

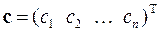Подстановка её решения в граничные условия краевой задачи при x = 0 и x = l даёт n алгебраических уравнений относительно постоянных с ₁, с ₂,…, с_n

↔

↔

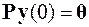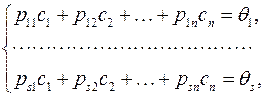
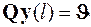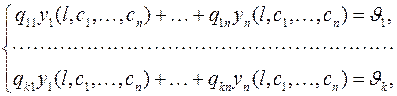
Первая система из s уравнений является линейной, а для конкретизации второй системы из k уравнений надо воспользоваться свойствами линейных систем обыкновенных дифференциальных уравнений. Как известно из теории дифференциальных уравнений общее решение таких систем является линейной комбинацией их линейно независимых частных решений

,

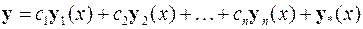где

, ,

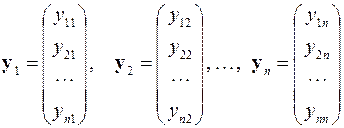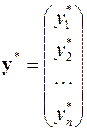или

,

где квадратная матрица Y ₀ составлена из частных решений однородной системы уравнений

.

В связи с этим вторая система уравнений, получающаяся из граничных условий при x = l, тоже будет линейной – системой линейных алгебраических уравнений

:

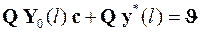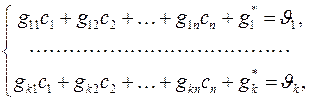
где

.

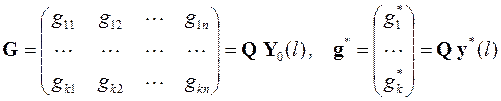Отсюда, из сравнения структуры решения нормальной системы линейных дифференциальных уравнений и структуры системы линейных алгебраических уравнений, получающихся из граничных условий при x = l, можно построить следующий алгоритм нахождения коэффициентов матрицы G и вектора g ^*.

Сначала задача Коши численно решается для нулевых начальных условий. В этом случае все слагаемые с постоянными с ₁, с ₂,…, с_n и в решении задачи Коши, и в граничных условиях при x = l, будут отсутствовать. Поэтому с помощью такого решения появляется возможность найти элементы вектора g ^*:

.

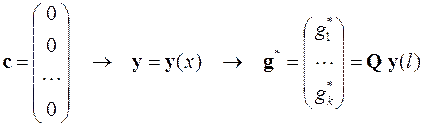Затем задача Коши численно решается ещё n раз с единичными начальными условиями. Под такими начальными условиями имеются в виду условия, у которых одна компонента равна единице, а остальные считаются равными нулю. По этим решениям находятся элементы столбцов матрицы G:

,

,

………………………………………………………….

.

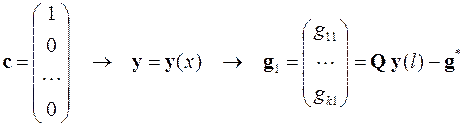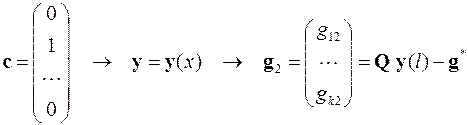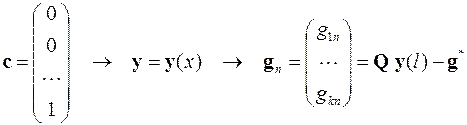После этого системы линейных алгебраических уравнений, полученные из граничных условий при x = 0 и x = l, объединяются в одну систему из n уравнений

,

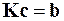где

,

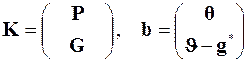которая решается одним из известных методов решения систем линейных алгебраических уравнений и, таким образом, определяются постоянных с ₁, с ₂,…, с_n.

Иллюстрацией данному алгоритму может служить решение следующей краевой задачи для линейного уравнения 2-го порядка

, .

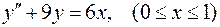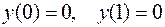Сначала эта задача приводится к краевой задаче для нормальной системы дифференциальных уравнений

, ,

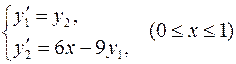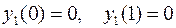где введены обозначения 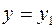, 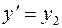. В матричной форме она имеет вид

,

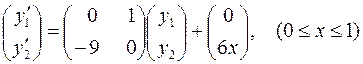при x = 0: 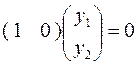, при x = l: .

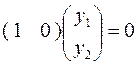Здесь

.

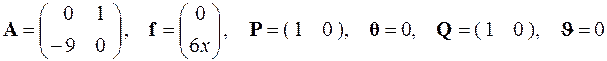Затем для неё записывается эквивалентная задача Коши

,

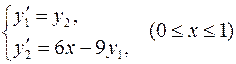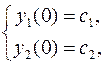
которая решается трижды для следующих начальных условий

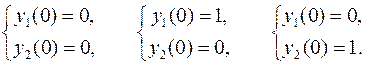
Её решение методом Эйлера для первой пары начальных условий даёт следующие значения y ₁(x) и y ₂(x), которые сведены в таблицу

x		0.1	0.2	0.3	0.4	0.5	0.6	0.7	0.8	0.9	1.0
y 1	0.000	0.000	0.000	0.006	0.024	0.060	0.117	0.199	0.306	0.438	0.5897
y 2	0.000	0.000	0.060	0.180	0.355	0.573	0.820	1.074	1.316	1.520	1.666

Повторное решение этой же задачи для второй и третьей пар начальных условий даёт другие значения y ₁(x) и y ₂(x), которые также сведены в таблицы

x		0.1	0.2	0.3	0.4	0.5	0.6	0.7	0.8	0.9	1.0
y 1	1.000	1.000	0.910	0.736	0.492	0.200	–0.112	–0.413	–0.667	–0.842	–0.909
y 2	0.000	–0.900	–1.740	–2.439	–2.921	–3.124	–3.004	–2.543	–1.751	–0.671	0.627

x		0.1	0.2	0.3	0.4	0.5	0.6	0.7	0.8	0.9	1.0
y 1	0.000	0.100	0.200	0.297	0.388	0.470	0.542	0.601	0.647	0.681	0.7051
y 2	1.000	1.000	0.970	0.910	0.823	0.714	0.590	0.463	0.342	0.240	0.1670

Значит

,

,

.

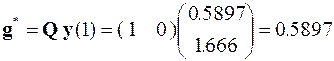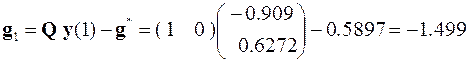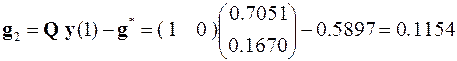Поэтому система линейных алгебраических уравнений для определения постоянных с ₁ и с ₂ будет иметь вид

.

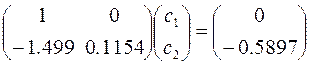Её решение легко находится

.

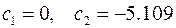С полученными значениями с ₁ и с ₂ методом Эйлера строится окончательное решение задачи Коши. Оно приведено в следующей таблице.

x		0.1	0.2	0.3	0.4	0.5	0.6	0.7	0.8	0.9	1.0
y 1	0.000	–0.511	–1.022	–1.481	–1.836	–2.039	–2.054	–1.855	–1.435	–0.806	0.000
y 2	–5.109	–5.109	–4.589	–3.549	–2.037	–0.145	1.991	4.199	6.288	8.059	9.324

Из неё видно, что на левом (при x = 0) и на правом (при x = 1) концах отрезка поиска решения заданной краевой задачи получено равенство искомого решения нулю.

Оценка погрешности метода стрельбы

Основной вклад в ошибку приближённых решений краевых задач получаемых методом стрельбы вносят методы решения задачи Коши. На каждом шаге h по аргументу x они вносят в решение абсолютную погрешность, оцениваемую неравенством

,

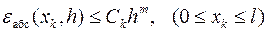где m = 2 для метода Эйлера, m = 3 для усовершенствованного метода Эйлера и m = 5 для метода Рунге-Кутта 4-го порядка. Абсолютная погрешность приближённого решения на всём отрезке интегрирования системы дифференциальных уравнений описывается неравенством

,

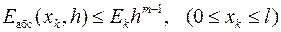Однако на практике из-за необходимости вычисления C_k и E_k такая оценка абсолютных погрешностей решения краевой задачи затруднительна. Поэтому для вычисления погрешности рассматриваемых методов на всём отрезке поиска решения используют апостериорную оценку, базирующуюся на правиле Рунге

,

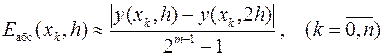где y (x_k, h) и y (x_k, 2 h) – приближённые значения решения, вычисленные в точке x_k при шагах интегрирования или разбиения отрезка поиска решения краевой задачи, отличающихся друг от друга в два раза. В качестве относительной погрешности решения краевой задачи используют её интервальную оценку

.

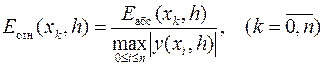Такой подход вполне оправдан до тех пор, пока при реализации вычислений не начинают сказываться неустранимые ошибки округления.

Дата добавления: 2014-12-16