Пример решения на ПЭВМ. Условия задачи. Найти решение краевой задачи

Условия задачи. Найти решение краевой задачи

,

.

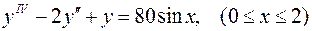Решение задачи построить так, чтобы его относительная погрешность не превышала бы 0.01%.

Решение. Для численного решения исходной краевой задачи её необходимо преобразовать к эквивалентной задаче Коши для нормальной системы дифференциальных уравнений. Это достигается путём введения следующего обозначения искомого решения и его производных

.

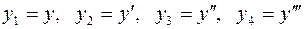В результате получается эквивалентная краевая задача

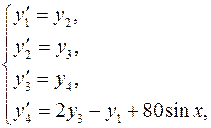
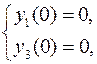
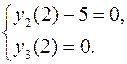
Ниже приведён текст программы, позволяющей получить численное решение рассматриваемой краевой задачи

xin=linspace(0,2,3); yin=[0;0;0;0];

init=bvpinit(xin,yin);

opt=bvpset('reltol',1.0e-4,);

sl=bvp4c(@fxy,@gru,init,opt);

fw=fopen('Lr_08.res','w');

m=length(sl.x);

for i=1:m;

fprintf(fw,'x=%4.2f y=%7.4f\n',...

sl.x(i),sl.y(1,i));

end;

fclose(fw);

plot(sl.x,sl.y(1,:),'-k',sl.x,sl.y(2,:),...

'--k',sl.x,sl.y(3,:),':k');

grid on; xlabel('x'); ylabel('y');

legend('y1','y2','y3',0);

Правые части системы дифференциальных уравнений описываются в функции fxy

function f=fxy(x,y)

f(1)=y(2);

f(2)=y(3);

f(3)=y(4);

f(4)=2*y(3)-y(1)+80*sin(x);

end

а граничные условия – в функции gru

function g=gru(y0,y2)

g(1)=y0(1);

g(2)=y0(3);

g(3)=y2(2)-5;

g(4)=y2(3);

end

В процессе выполнения программы осуществляется пошаговая печать в файл Lr_08.res. В результате он будет заполнен следующей информацией

x=0.00 y= 0.0000

x=0.08 y= 1.7538

x=0.17 y= 3.4981

x=0.33 y= 6.9213

x=0.50 y=10.1980

x=0.67 y=13.2633

.................

x=2.00 y=27.0532

Графики численного решения рассматриваемой краевой задачи, получающиеся в графическом окне Matlab’а, представлены на рис.1.

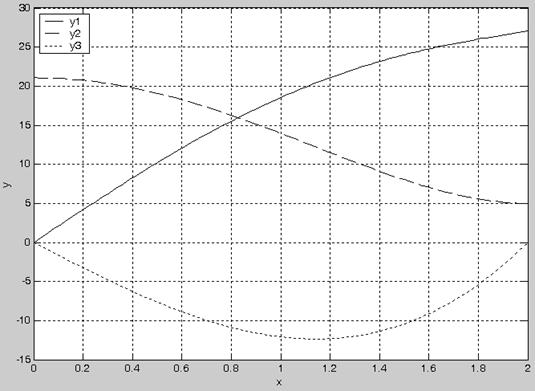
Рис.1.

Контрольные задания

Получить решение краевой задачи на указанном отрезке c относительной погрешностью, не превышающей 0.1%. Построить графики полученного решения.

1. .

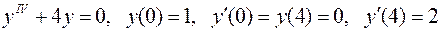2.

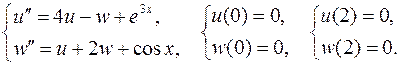
3. .

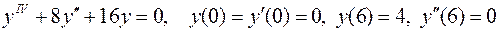4. .

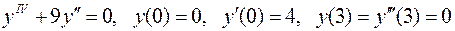5. .

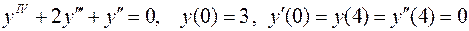6.

7. .

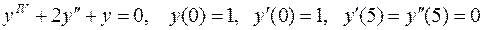8. .

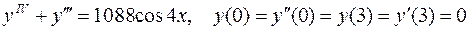9.

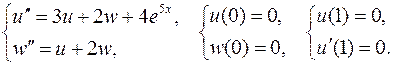
10. .

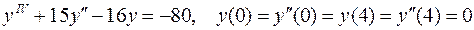11.

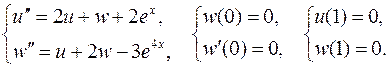
12. .

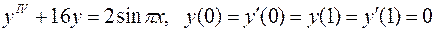13. .

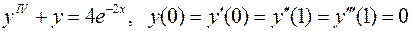14. .

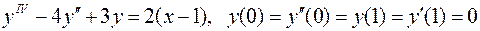15.

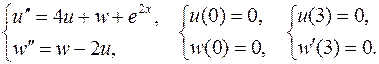
16. .

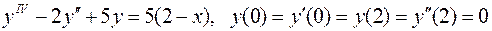17. .

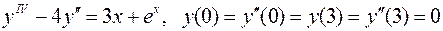18.

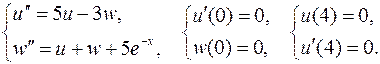
19. .

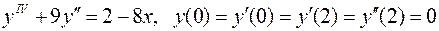20. .

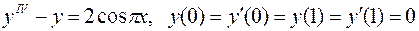21.

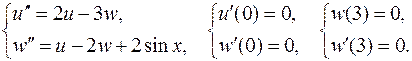
22. .

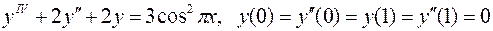23. .

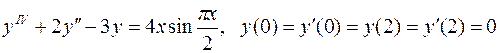24.

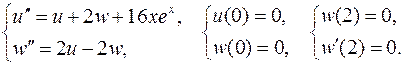
25. .

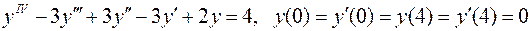26. .

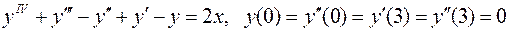27.

28. .

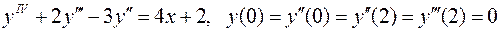29. .

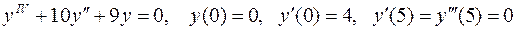30.

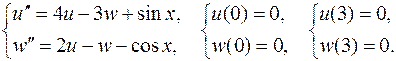
Дата добавления: 2014-12-16