Вероятность суммы событий

Теорема 2.1. Вероятность суммы двух несовместных событий равна сумме вероятностей этих событий:

Теорема 2.2. Для любого события А вероятность противоположного события А выражается равенством

Р (` А) = 1 – Р (А)

Теорема 2.3. Вероятность суммы двух совместных событий равна сумме вероятностей этих событий минус вероятность их совместного появления:

Р (А + В) = Р (А) + Р (В) – Р (АВ).

Теорема сложения обобщается на любое конечное число событий следующим образом:

(2.3)

Если события А ₁, А ₂,..., А_ппопарно несовместные, то формула (2.3) принимает вид:

Замечание. При решении задач с использованием формулы (2.3) приходится производить громоздкие вычисления, поэтому часто выгоднее перейти к противоположным событиям, т.е. вместо вероятности суммы событий А ₁ +А ₂ +...+А_п находить вероятность произведения противоположного события . Очевидно, что эти два события противоположны, поэтому

(2.4)

Пример 2.13. В условиях примера 2 предыдущего пункта найти вероятность появления хотя бы одной пробоины.

Решение. Данное событие есть сумма событий А и В, причем эти события совместные, поэтому вероятность интересующего нас события равна Р (А + В) = Р (А) + Р (В) – Р (АВ). Ранее было найдено, что Р (АВ) = 0.48, следовательно, Р(А + В) = 0.6 + 0.8 – 0.48 = 0.92.

Пример 2.14. Устройство содержит четыре независимо работающих элемента и сохраняет работоспособность, если работает хотя бы один из элементов. Вероятности безотказной работы элементов в течение определенного срока соответственно равны 0.9, 0.8, 0.7 и 0.6. Найти вероятность безотказной работы устройства.

Решение. Пусть события А ₁ А ₂, А ₃и А ₄означают безотказную работу соответственно первого, второго, третьего и четвертого элементов. Событие А= {безотказная работа устройства} есть сумма событий: А=А ₁ +А ₂ +А ₃ +А ₄.События А ₁ А ₂, А ₃и А ₄совместные, поэтому вероятность Р (А)надо вычислять по формуле (2.3). Чтобы упростить вычисления, воспользуемся формулой (2.4):

.

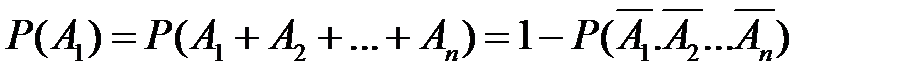Так как события А ₁ А ₂, А ₃и А ₄независимые, то противоположные события 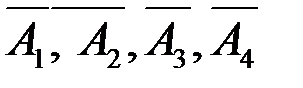также независимы, поэтому

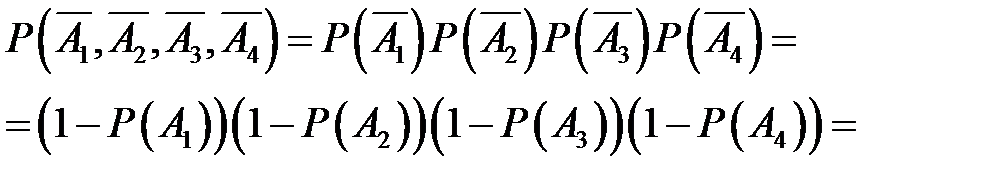
= (1 – 0.9)(1 – 0.8)(1 – 0.7)(1 – 0.6) = 0.0024; и

Р (А) = 1 – 0.0024 = 0.9976.

Пример 2.15. Производится три независимых выстрела по мишени. Вероятности попадания в мишень при первом, втором и третьем выстрелах соответственно равны 0.2, 0.5, 0.4. Найти вероятность того, что будет ровно два попадания в мишень.

Решение. Событие А= { ровно два попадания в мишень} выражается через события А ₁ = {попадание при первом выстреле}, А ₂={попадание при втором выстреле), А ₃={попадание при третьем выстреле} следующим образом:

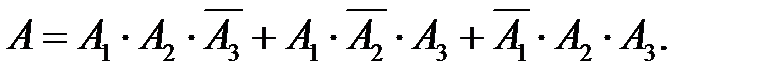
Отсюда, учитывая несовместность суммируемых произведений событий и независимость событий А ₁, А ₂, А ₃,находим

Пример 2.16. В двух урнах находятся шары, отличающиеся только цветом: в первой урне 5 белых шаров, 11 черных и 8 красных, во второй 10 белых, 8 черных и 6 красных. Из обеих урн наудачу извлекают по одному шару. Найти вероятность того, что оба шара одного цвета.

Решение. Введем в рассмотрение следующие события:

В ₁={извлечение белого шара из первой урны},

В ₂={извлечение белого шара из второй урны},

С ₁={извлечение черного шара из первой урны},

С ₂={извлечение черного шара из второй урны},

D ₁={извлечение красного шара из первой урны},

D ₂={извлечение красного шара из второй урны}.

Выразим событие А= {извлечение шаров одного цвета} через эти события:

А= В ₁ В ₂+ С ₁ С ₂+ D ₁ D ₂

Следовательно,

Р (А) = Р (В ₁) Р (В₂) + Р (С ₁) Р (С ₂) + Р (D ₁) P (D₂).

Вероятности событий В, С, D найдем из классического определения: Р (В ₁)=5/24, Р (В₂)=10/24, Р (С ₁)=11/24, Р (С ₂)=8/24, Р (D ₁)=8/24, P (D₂)= 6/24.

Таким образом, получаем

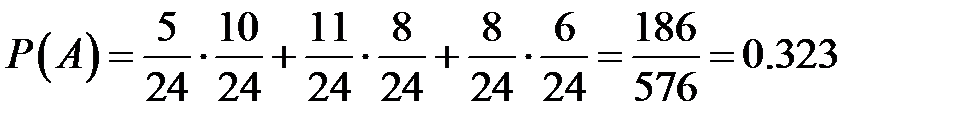
Дата добавления: 2014-12-16