Закон распределения дискретной случайной величины

Понятие случайной величины

СЛУЧАЙНЫЕ ВЕЛИЧИНЫ

Случайной величиной называется величина, которая в результате испытаний, проводимых в одних и тех же условиях, принимает различные, вообще говоря, значения, зависящие от не учитываемых случайных факторов. Примеры случайных величин: число выпавших очков на игральной кости, число дефектных изделий в партии, отклонение точки падения снаряда от цели, время безотказной работы устройства и т.п. Различают дискретные и непрерывные случайные величины. Дискретной называется случайная величина, возможные значения которой образуют счетное множество, конечное или бесконечное (т.е. такое множество, элементы которого могут быть занумерованы).

Непрерывной называется случайная величина, возможные значения которой непрерывным образом заполняют некоторый конечный или бесконечный интервал числовой оси. Число значений непрерывной случайной величины всегда бесконечно.

Случайные величины будем обозначать заглавными буквами конца латинского алфавита: X, Y,...; значения случайной величины – строчными буквами: х, у,.... Таким образом, X обозначает всю совокупность возможных значений случайной величины, а х – некоторое ее конкретное значение.

Законом распределения дискретной случайной величины называется задаваемое в любой форме соответствие между возможными значениями случайной величины и их вероятностями.

Пусть возможными значениями случайной величины X являются 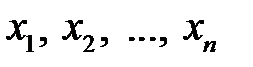. В результате испытания случайная величина примет одно из этих значений, т.е. произойдет одно событие из полной группы попарно несовместных событий.

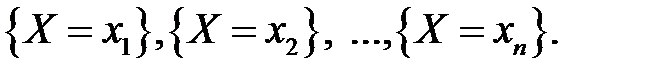
Пусть также известны вероятности этих событий:

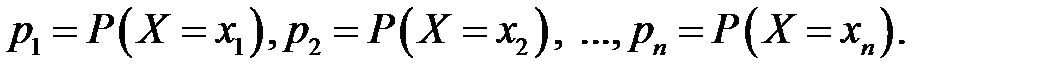
Закон распределения случайной величины X может быть записан в виде таблицы, которую называют рядом распределения дискретной случайной величины:

X	x 1	x 2	…	x 3
p	p 1	p 2	…	p 3

Для ряда распределения имеет место равенство 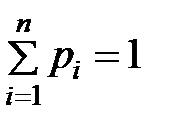(условие нормировки).

Пример 3.1. Найти закон распределения дискретной случайной величины X – числа появлений «орла» при двух бросаниях монеты.

Решение. Возможные значения случайной величины: 0, 1, 2. Вероятности этих значений находим по формуле Бернулли:

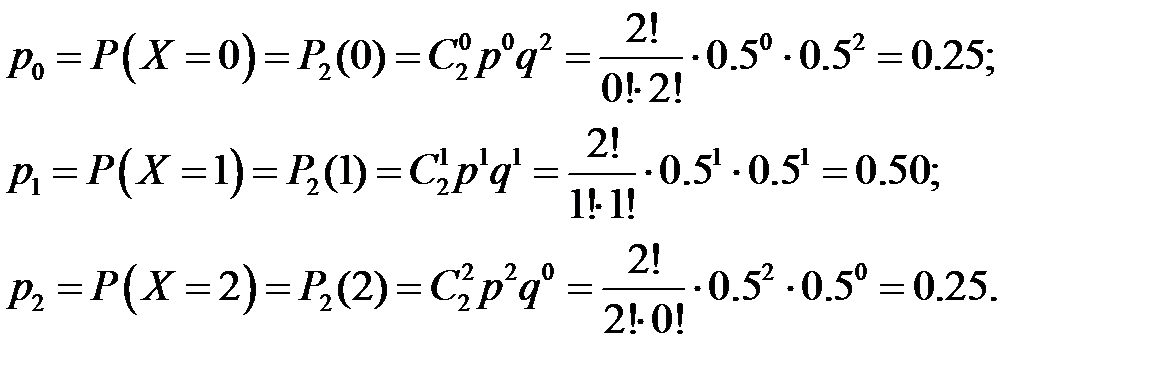
Записываем ряд распределения:

X
p	0.25	0.50	0.25

Дата добавления: 2014-12-16