Критерии работоспособности и устойчивости

Работа замкнутой системы управления второго порядка основана на критериях:

· обеспечение хорошей динамики;

· небольшая или нулевая статическая ошибка;

· малое время переходных процессов.

Предполагаем, что возмущения отсутствуют. Тогда из уравнения (17-7) видно, что мы имеем систему второго порядка с нулевым корнем. Характеристическое уравнение системы второго порядка может быть записано в стандартной форме:

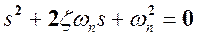, (17-8)

где 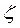и - соответственно коэффициент демпфирования и собственная частота колебаний системы;

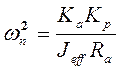(17-9)

и . (17-10)

Работа системы второго порядка определяется значениями ее собственной частоты колебаний и коэффициентом демпфирования 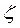. Для устранения колебаний и резонанса конструкции сочленения необходимо выбирать значение частоты собственных колебаний, не превышающих половины величины резонансной частоты конструкции сочленения: , где - резонансная частота конструкции сочленения, (рад/с). Резонансная частота конструкции зависит от материала, из которого изготовлен манипулятор. Если эффективную жесткость сочленения обозначить , то возвращающий момент противодействует моменту инерции двигателя:

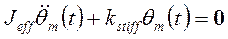. (17-11)

Произведя преобразование Лапласа, получим характеристическое уравнение выражения (17-11) в виде:

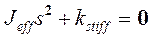. (17-12)

Решение этого уравнения дает резонансную частоту конструкции системы:

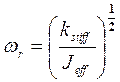. (17-13)

Для того, чтобы скомпенсировать силы тяжести и центробежные силы, можно вычислить величины моментов от них и эти значения подать в устройство управления, как это показано на рис. 17.3, с целью минимизации их влияния. Такая компенсация называется компенсацией по прямой связи.

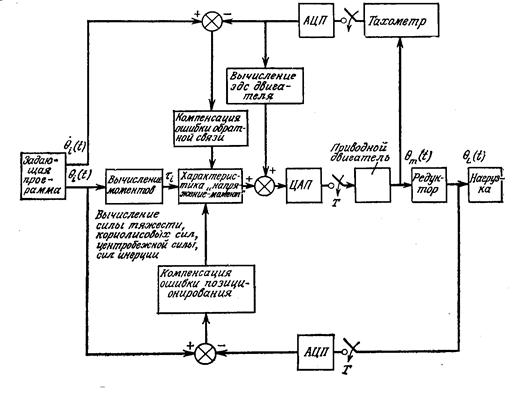
Рисунок 17.3. Компенсация возмущений

Если момент компенсации 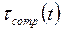создается только силой тяжести звена манипулятора, выражение для статической ошибки позиционирования:

, (17-14)

где 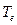- момент, выраженный через преобразование Лапласа.

В общем случае уравнения Лагранжа-Эйлера, описывающие движение манипулятора с шестью сочленениями без учета динамики электронного управляющего блока, трения в редукторе и люфтов, могут быть записаны в виде, соответствующем уравнению (10-11):

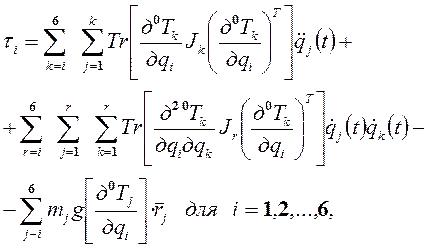(17-15)

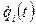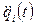где - обобщенный управляющий момент в i -м сочленении для перемещения i -го звена; и - соответственно угловая скорость и угловое ускорение i -го сочленения; - обобщенная координата манипулятора, определяющая его угловое положение; - однородная матрица преобразования для звена размерностью 4×4, которая связывает пространственное расположение между двумя системами координат (i -й и базовой); - положение центра масс i -го звена относительно i -й координаты системы; - линейный вектор силы тяжести, ; 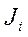- матрица псевдоинерции i-го звена относительно системы координат i-го звена, которая может быть записана в соответствии с уравнением (10-5).

Эта компенсация соответствует тому, что обычно называют методом обратной задачи динамики или методом вычисления момента.

Дата добавления: 2014-12-17