Кинематика звеньев

Выведем уравнения, основывающиеся на полученных ранее соотношениях для подвижной системы координат и описывающие кинематику звеньев манипулятора в базовой системе координат.

Известно, что ортонормированная система координат 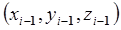связана с осью i -го сочленения (рис. 12.2).

Рисунок 12.2. Взаимосвязь систем координат,

имеющих начала в точках 0, 0^* и 0'

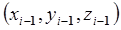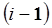Системы координат и связаны с -м и i -м звеньями и имеют начала в точках 0^* и 0' соответственно. Положение точек 0' и 0^* в базовой системе координат определяется векторами р _i и р _i-1 соответственно. Относительное положение точек 0' и 0^* характеризуется в базовой системе координат вектором .

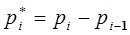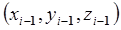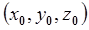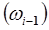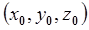Предположим, что система координат имеет относительно базовой системы координат линейную скорость и угловую скорость . Пусть и - угловые скорости точки 0' в системах координат и 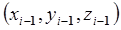соответственно. Тогда линейная скорость и угловая скорость координат относительно базовой системы координат с учетом равенства (12-3) определяются выражениями:

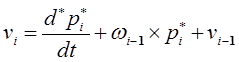, (12-6)

, (12-7)

где означает скорость в движущейся системе координат 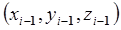. Линейное ускорение 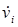и угловое ускорение 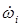системы координат относительно базовой системы координат с учетом равенства (12-5) определяются выражениями:

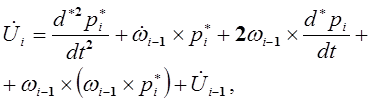(12-8)

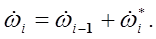(12-9)

Пользуясь равенством (11-13), находим угловое ускорение системы координат относительно системы координат :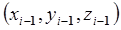

. (12-10)

В результате равенство (12-9) можно представить в следующем виде:

. (12-11)

Как уже говорилось, системы координат 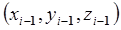и в соответствии с алгоритмом формирования систем координат звеньев манипулятора связаны с 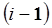-м и i -м звеньями соответственно. Если i- е сочленение – поступательное, то i- е звено совершает поступательное движение вдоль оси 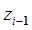со скоростью 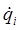относительно 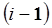-го звена. Если i- е сочленение – вращательное, то i- е звено вращается вокруг оси 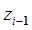с угловой скоростью относительно 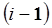-го звена.

Таким образом,

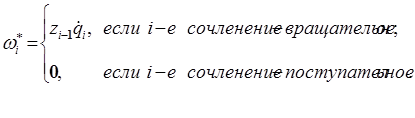. (12-12)

Здесь 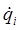- величина угловой скорости вращения i- го звена относительно системы координат 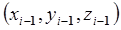. Аналогично:

. (12-13)

С учетом равенств (12-12) и (12-13) формулы (12-7) и (12-11) могут быть представлены в следующем виде:

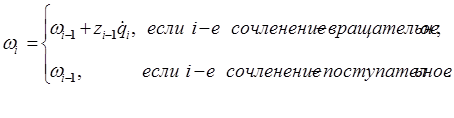; (12-14)

.(12-15)

С учетом равенства (11-8) линейные скорость и ускорение i- го звена относительно 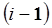-го можно представить в следующем виде:

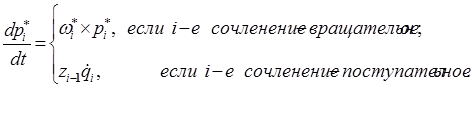. (12-16)

.

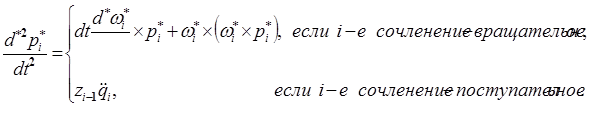(12-17)

Используя равенства (12-16) и (12-7), выражение (12-6) для линейной скорости i- го звена относительно базовой системы координат можно представить в виде:

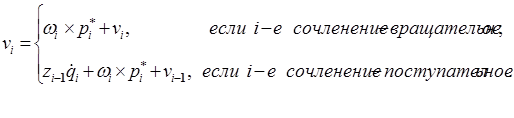.(12-18)

Выражение (12-8) для линейного ускорения i- го звена относительно базовой системы координат с учетом следующих свойств векторного произведения:

, (12-19)

(12-20)

и равенств (12-12) – (12-17) преобразуется к виду:

(12-35)

Заметим, что , если i- е сочленение – поступательное. Равенства (12-14), (12-15), (12-18) и (12-21), описывающие кинематику движения i- го звена, потребуется нам при выводе уравнений динамики манипулятора.

Дата добавления: 2014-12-17