Задачи динамики для свободной и несвободной мате­риальной точки

Для свободной материальной точки задачами дина­мики являются следующие: 1) зная закон движения точки, определить действующую на нее силу (первая задача динамики); 2) зная дей­ствующие на точку силы, определить закон движения точки (вторая или основная задача динамики).

Решаются обе эти задачи с помощью уравнений, вы­ражающих основной закон динамики, так как эти уравнения связывают ускорение а т. е. величину, характеризующую движение точки, и действующие на нее силы.

В технике часто приходится сталкиваться с изучением несвобод­ного движения точки, т. е. со случаями, когда точка, благодаря на­ложенным на нее связям, вынуждена двигаться по заданной неподвиж­ной поверхности или кривой.

В этих случаях, как и в статике, будем при решении задач исхо­дить из аксиомы связей, согласно которой всякую несвободную ма­териальную точку можно рассматривать как свободную, отбросив связь и заменив ее действие реакцией этой связи N. Тогда основной закон динамики для несвободного движения точки примет вид:

ma = ΣF_k^a+N,

где F_K^a -действующие на точку активные силы.

Первая задача динамики для несвободного движения будет обычно сводиться к тому, чтобы, зная движение точки и действующие на нее активные силы, определить реакцию связи.

Пример решения первой задачи динамики: Лифт весом Р (рис. 1) начинает подниматься с ускоре­нием а. Определить натяжение троса.

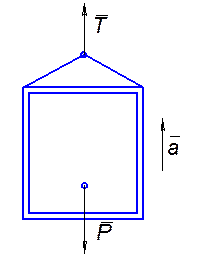
Рисунок 1

Рассматривая лифт как свободный, заменяем действие связи (троса) реакцией Т и, составляя уравнение ma = ΣF_k^a + N в проекции на вертикаль, получаем:

.

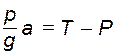Отсюда находим: .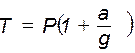

Если лифт начнёт опускаться с таким же ускорением, то натяжение троса будет равно:

.

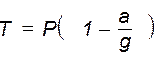Дата добавления: 2014-12-17