Теорема об изменении количества движения точки

Так как масса точки постоянна, а ее ускорение то уравне­ние, выражающее основной закон динамики, можно представить в виде

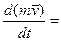Σ .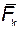

Уравнение выражает одновременно теорему об изменении количества движения точки в дифференциальной форме: производная

по времени от количества движения

точки равна геометрической сумме

действующих на точку сил.

Проинтегрируем это уравнение.

Пусть точка массы т, движущаяся

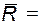под действием силы ΣF_k

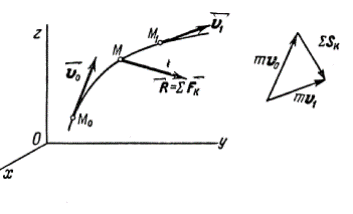
(рис.4), имеет в момент t=0

Рисунок 4

скорость v ₀,, а в момент

t₁-скорость v₁. Умножим тогда обе части равенства на dt и возь­мем от них определенные интегралы. При этом справа, где интегри­рование идет по времени, пределами интегралов будут 0 и t₁, а слева, где интегрируется скорость, пределами интеграла будут соответствую­щие значения скорости v₀

t₁

и v₁. Так как интеграл от d(m v ) равен mv, то в результате получим:

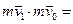Σ ₀∫ .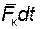

Стоящие справа интегралы пред­ставляют собою импульсы действующих сил. Поэтому окончательно будем иметь:

∑ .

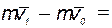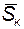Уравнение выражает теорему об изменении коли­чества движения точки в конечном виде: изменение коли­чества движения точки за некоторый промежуток времени равно геометрической сумме импульсов всех действующих на точку сил за тот же промежуток времени ( рис. 4).

При решении задач вместо векторного уравнения часто пользуются уравнениями в проекциях.

∑ ;

∑ ;

∑ .

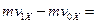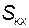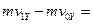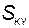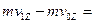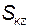В случае прямолинейного движения, происходящего вдоль оси Ох теорема выражается первым из этих уравнений.

ЛЕКЦИЯ 10

Дата добавления: 2014-12-17