Свободные колебания без учета сил сопротивления

ПРЯМОЛИНЕЙНЫЕ КОЛЕБАНИЯ ТОЧКИ

Изучение данных вопросов необходимо для динамики колебательного движения механических систем, теории удара, для решения задач в дисциплинах «Сопротивление материалов» и «Детали машин».

Учение о колебаниях составляет основу ряда областей физики и тех­ники. Хотя колебания, рассматриваемые в различных областях, на­пример в механике, радиотехнике, акустике и др., отличаются друг от друга по своей физической природе, основные законы этих коле­баний во всех случаях остаются одними и теми же. Поэтому изуче­ние механических колебаний является важным не только по той причине, что такие колебания очень часто имеют место в технике, но и вследствие того, что результаты, полученные при изучении меха­нических колебаний, могут быть использованы для изучения и уясне­ния колебательных явлений в других областях.

Начнем с изучения свободных колебаний точки без учета сил сопротивления. Рассмотрим точку М, движущуюся прямолинейно под действием одной только восстанавливающей силы 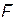, направленной к неподвижному центру. О и пропорциональной расстоянию от этого центра. Проекция силы 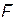на ось Ох (рис.14)

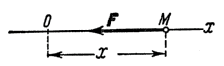будет равна

Рисунок.14

F_x=-cx.

Сила , как видим, стремится вернуть точку в равновесное положение О, где F=0;

отсюда и наименование «восстанавливающая» сила. Примером такой силы является сила упругости.

Найдем закон движения точки М. Составляя дифференциальное уравнение движения получим

.

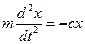Деля обе части равенства на т и вводя обозначение

,

приведем уравнение к виду

.

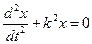Уравнение представляет собою дифференциальное уравне­ние свободных колебаний при отсутствии сопротивления. Реше­ние этого линейного однородного дифференциального уравнения второго порядка ищут в виде x=e^nt. Полагая x=e^nt, получим для определения п так называемое характеристиче­ское уравнение, имеющее в данном случае вид п² + k² = 0. Поскольку корни этого характеристического уравнения являются чисто мнимыми (n_1,2= ±ik), то, как известно из теории дифференциальных уравне­ний, общее решение имеет вид

х = C₁Sinkt + C₂Coskt,

где C₁ и С₂-постоянные интегрирования. Если вместо постоянных C₁ и С₂ ввести постоянные а и α, такие, что C₁=a Cosα, С₂=а Sinα, то мы получим x=a(sinkt cosα 4+ cos kt sinα) или

x=aSin(kt+α).

Это другой вид решения в котором постоянными интегрирования являются а и а. Им удобнее пользоваться для общих исследований.

Скорость точки в рассматриваемом движении равна

.

Колебания, совершаемые точкой по закону называются гар­моническими колебаниями.

Всем характеристикам этого движения можно дать наглядную ки­нематическую интерпретацию. Рассмотрим точку В, движущуюся равномерно по окружности радиуса а из положения В₀ определяемого углом DOВ₀ = α (рис.15) Пусть постоянная угловая ско­рость

вращения радиуса ОВ равна k. Тогда в произвольный

момент времени t угол φ = < DOB =α + kt и

про­екция М точки В на диаметр, перпендику­лярный к

DE, движется по закону х= а Sin (kt+α), где х=ОМ,

т. е. совер­шает гармонические колебания.

Рисунок.15

Величина а, равная наибольшему откло­нению точки М

от центра колебаний, назы­вается амплитудой

колебаний. Величина φ= α + kt называется фазой

колебаний.

Величина k, совпадающая с угловой скоростью вращения радиуса ОВ, показанного на рис.15 называется круговой частотой колебаний.

Промежуток времени Т (или τ), в течение которого точка совер­шает одно полное колебание, называется периодом колебаний.

По истечении периода фаза изменяется на 2π. Следовательно, должно kT=2π откуда период

.

Величина υ, обратная периоду и определяющая число колебаний, совершаемых за одну секунду, называется частотой колебаний

υ .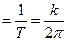

Отсюда видно, что величина k отличается от Т только постоянным множителем 2π. В дальнейшем мы обычно для краткости частотой колебаний будем называть величину k.

Значения а и α определяются по начальным условиям. Считая при t=0 x=x₀, V_X=V₀ получим x₀,= aSinα и 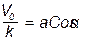. Отсюда, складывая сначала квадраты этих равенств,а затем деля их почленно, найдем:

.

Отметим, что свободные колебания при отсутствии сопротивления обладают следующими свойствами: 1) амплитуда и начальная фаза колебаний зависят от начальных условий; 2) частота k,, а следова­тельно, и период Т колебаний от начальных условий не зависят.

Влияние постоянной силы на свободные колебания

точки. Пусть на точку М, кроме восстанавливающей

силы F, направленной к центру О, действует еще

постоянная по модулю и направлению сила Р

Рисунок.16

(рис.16). Ве­личина силы F попрежнему пропорциональна расстоянию от центра О,т.е.

Очевидно, что в этом случае положением рав­новесия точки М будет центр О₁ отстоящий от О на расстоянии ОО₁=δ_ст, которое определяется равенством сδ_ст=Р или

.

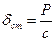Величину δ_ст назовем статическим отклонением точки. Примем центр O₁ за начало отсчета и направим координатную ось О₁х в сторону действия силы Р. Тогда F_X=- с(x+δ_ст), P_X=P. В результате, составляя дифференциальное уравнение дви­жения и учитывая, что согласно равенству сδ_ст=Р, будем иметь:

.

Отсюда заключаем, что постоянная сила Р не изменяет характера колебаний, совершаемых точкой под действием восстанавливающей силы F, а только смещает центр этих колебаний в сторону действия силы Р на величину ста­тического отклонения δ_ст

Дата добавления: 2014-12-17