Работа силы. Мощность. Для характеристики действия, оказываемого силой на тело при некотором его перемещении, вводится понятие о работе силы

Для характеристики действия, оказываемого силой на тело при некотором его перемещении, вводится понятие о работе силы.

При этом работа характеризует то действие силы, которым определяется изменение модуля скорости движущейся точки.

Введём сначала понятие об элементарной работе силы на

Рисунок.5

бесконечно малом перемещении ds. Элементарной работой силы F (рис.5) называется скалярная величина:

dA=F_τds,

где F_τ -прекция силы F на касательную к тректории, направленную в сторону перемещения точки, а ds-бесконечно малое перемещение точки, направленное вдоль этой касательной.

Данное определение соответствует понятию о работе, как о ха­рактеристике того действия силы, которое приводит к изменению модуля скорости точки. В самом деле, если разложить силу F на составляющие F_τ и F_n, то изменять модуль скорости точки будет только составляющая F_τ, сообщающая точке касательное ускорение Составляющая же F_n или изменяет направление вектора скорости v (сообщает точке нормальное ускорение), или, при несвободном дви­жение изменяет давление на связь. На модуль скорости составляю­щая F_n влиять не будет, т.е., как говорят, сила F _n «не будет про­изводить работу».

Замечая, что F_τ=Fcosα, получаем: .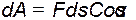

Таким образом, элементарная работа силы равна проекции силы на направление перемещения точки, умноженной на элементар­ное перемещение ds или элементарная работа силы равна произведению модуля силы на элементарное перемещение ds и на косинус угла между направлением силы и направлением перемещения.

Если угол а острый, то работа положительна. В частности, при α=0 элементарная работа dA=Fds.

Если угол α тупой, то работа отрицательна. В частности, при α=180˚ элементарная работа dA=-F ds.

Если угол α=90˚, т. е. если сила направлена перпендикулярно перемещению, то элементарная работа силы равна нулю.

Найдем аналитическое выражение элементарной работы. Для этого разложим силу F на составляющие F_X, F_Y, F_Z по направлениям координатных

осей (рис.6; сама сила F на чертеже не показана).

Элементарное перемещение ММ’=ds слагается из

перемещений dz, dy, dz вдоль координатных осей,

где x, y, z-координаты точки М. Тогда работу

силы F на перемещении ds можно вычислить как

сумму работ её составляющих F_X, F_Y, F_Z на

перемещениях dz, dy, dz. Но на перемещении dx

Рисунок 6

совершает работу только составляющая F_X,

причём её работа равна F_Xdx. Работа на

перемещениях dy и dz вычисляется аналогично.

Окончательно находим: dA=F_X dx+F_Ydy+F_Zdz.

Формула дает аналитическое выражение элементарной работы силы.

Работа силы на любом конечном перемещении М₀М₁ вычисляется как интегральная сумма соответствующих элементарных работ и будет равна:

А_(М0М1)=∫F_τds
или

А_(М0М1)= ∫(F_xdx+F_ydy+F_zdz).

Следовательно, работа силы на любом перемещении М₀М₁ равна взятому вдоль этого перемещения интегралу от элементарной работы. Пределы интеграла соответствуют значениям пере­менных интегрирования в точках М₀ и М₁.

Если величина F_τ постоянна (F_τ = const), то и обозначая

перемеще­ние М₀М₁ через s₁ получим: А_(М0М1)= F_τs₁.

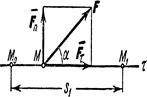
Такой случай может иметь место когда действующая

Рисунок 7

сила постоянна по модулю и направлению (F= const), а

точка, к ко­торой приложена сила, движется прямолинейно (рис.7}. В этом случае F_τ=F Сosα= const и работа силы А_(М0М1)=Fs₁cosα.

Единицей измерения работы в системе СИ является джоуль (1 дж= 1 hm).

Мощность. Мощностью называется величина, определяющая работу, совершаемую силой в единицу времени. Если работа совершается равномерно, то мощность

,

где t - время, в течение которого произведена работа A. В общем случае

.

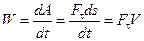Следовательно, мощность равна произведению касательной состав­ляющей силы на скорость движения.

Единицей измерения мощности в системе СИ является ватт (1 вт=1 дж/сек). В технике за единицу мощности часто принимается 1 лошадиная сила, равная 75 кГм/сек или 736 вт.

Работу, произведенную машиной, можно измерять произведением ее мощности на время работы. Отсюда возникла употребительная в технике единица измерения работы киловатт-час (1 квт-ч = 3,6 X 10⁶ дж~ 367100 кГм).

Из равенства W=F_τV видно, что у двигателя, имеющего дан­ную мощность W, сила тяги F_τ будет тем больше, чем меньше ско­рость движения V. Поэтому, например, на подъеме или на плохом участке дороги у автомобиля включают низшие передачи, позволяю­щие при полной мощности двигаться с меньшей скоростью и раз­вивать большую силу тяги.

Дата добавления: 2014-12-17