Таким образом, оказывается, что работа силы F

зависит только от значе­ний Δl_нач и Δl_кон и не

зависит от вида траектории точки М. Следовательно,

Рисунок.10

сила упругости также является потенциальной.

3) Р а б о т а силы трения. Рассмотрим точку, движущуюся

по какой-нибудь шероховатой поверхности (рис. 10) или кривой.

Действующая на точку сила трения равна по модулю fN, где f -коэффициент трения, а N-нормальная реакция поверхности. Направлена сила трения противоположно перемещению точки. Следовательно, F_тр.τ=-fN и по формуле

(M_1­)

(M₁)

(M₀)

(M₀)

А_(М0М1)=- ∫F_трds=-∫fNdx.

Если величина силы трения постоянна, то A_М0М1) = -F_трs, где s -длина дуги кривой М₀М₁ по которой перемещается точка.

Таким образом, работа силы трения при скольжении всегда отрицательна. Величина этой работы зависит от длины дуги М₀М₁.

Следовательно, сила трения является силой непотенциальной.

Теорема об изменении кинетической энергии точки

Рассмотрим точку с массой т, перемещающуюся под действием при­ложенных к ней сил из положения M₀, где она имеет скорость V₀,, в положение М₁, где ее скорость равна V ₁.

Для получения искомой зависимости обратимся к уравнению ma=ΣF_k выражающему основной закон динамики. Проектируя обе части этого равенства на касательную M_τ к траектории точ­ки М, направленную в сторону движения, получим:

mа=ΣF_kτ.

Стоящую слева величину касательного ускорения можно пред­ставить в виде

.

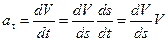В результате будем иметь:

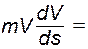ΣF_kτ.

Умножив обе части этого равенства на ds, внесем т под знак дифференциала. Тогда, замечая, что ΣF_kτds = dA_к где dA_k- эле­ментарная работа силы F_k получим выражение теоремы об изме­нении кинетической энергии в дифференциальной форме:

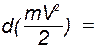ΣdA_k.

Проинтегрировав теперь обе части этого равенства в пределах, соответствующих значениям переменных в точках M₀ и M₁, найдем окончательно:

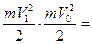Σ А_(М0М1).

Уравнение выражает теорему об изменении кине­тической энергии точки в конечном виде: изменение кинетической энергии точки при некотором ее перемещении равно алгебраической сумме работ всех действующих на точку сил на том же перемещении.

Теорема об изменении момента количества движения точки (теорема моментов)

Из двух основных динамических харак­теристик, величина mV является векторной. Иногда при изучении движения точки вместо изменения самого вектора mV оказывается необходимым рассматривать изменение его момента. Мо­мент вектора mV относительно данного центра О или оси z обозна­чается т_O ( mV ) или m_Z ( mV ) и называется соответственно моментом количества движения или кинетическим моментом точки отно­сительно этого центра (оси). Вычисляется момент вектора 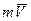так же, как и момент силы. При этом вектор mV считается приложенным к движущейся точке. По модулю

| т_O (mV) | = mVh, где h- длина перпендикуляра, опущенного из центра О на направление вектора m 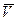(рис.10,a).

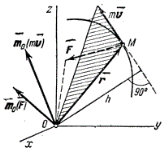
Теорема моментов отно­сительно центра. Найдем для

ма­териальной точки, движущейся под дей­ствием силы F

(рис.10,а), зависимость между моментами векторов

тV и F отно­сительно какой-нибудь неподвижного

центра О. В конце было показано, что

m₀(F)= .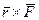

Аналогично т_O(mV)= .

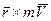При этом вектор m₀(F) направлен перпендикулярно

Рисунок.10,а

плоскости, проходящей через центр О и вектор F, а

вектор т_O(mV)- перпендикулярно плоскости, проходящей через центр О и вектор mV.

Дифференцируя выражение т_O(mV)по времени, получаем:

.

Но , как векторное произведение двух параллельных векторов, a 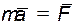. Следовательно,

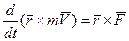
или .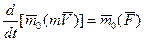

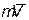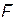В результате мы доказали следующую теорему моментов относительно центра: производная по времени от момента количества движения точки, взятого относительно какого-нибудь неподвижного центра, равна моменту действующей на точку силы относительно того же центра. Аналогичная теорема имеетместо для моментов вектора силы относительно какой-нибудь оси z, в чем можно убедиться, проектируя обе части равенства 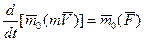на эту ось. Ма­тематическое выражение теоремы моментов относительно оси дается формулой .

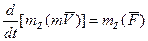Дата добавления: 2014-12-17