Таким образом, искомое частное решение будет

Тогда, учитывая обозначение, приведем уравнение движения к виду

.

Уравнение является дифференциальным уравнением вынуж­денных колебаний точки при отсутствии сопротивления. Его решением, как известно из теории дифференциальных уравнений, будет х = x₁+x₂, где х₁ -общее решение уравнения без правой части, а х₂- какое-нибудь частное решение полного уравнения.

Полагая, что p = k, будем искать решение х₂ в виде

x₂=Asinpt,

где А- постоянная величина, которую надо подобрать так, чтобы равенство обратилось в тождество. Подставляя значение х₂ и его второй производной в уравнение будем иметь:

-pASinpt+k²ASinpt=P₀Sinpt.

Это равенство будет выполняться при любом t, если A(k²-p²)=P₀ или

.

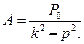
Так как х = х₁+x₂, а общее решение имеет окончательно вид

,

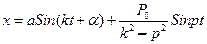где а и α - постоянные интегрирования, определяемые по начальным данным. Решение показывает, что колебания точки складываются в этом случае из: 1) колебаний с амплитудой а (зависящей от на­чальных условий) и частотой k, называемых собственными колеба­ниями, и 2) колебаний с амплитудой А (не зависящей от начальных условий) и частотой р, которые называются вынужденными колеба­ниями

Частота р вынужденных колебаний, как видно, равна частоте воз­мущающей силы. Амплитуду этих колебаний, если разделить числи­тель и знаменатель на k², можно представить в виде:

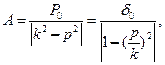
где , т. е. δ₀ есть величина статического отклонения точки под действием силы Q₀. Как видим, A зависит от отношения частоты р возмущающей силы к ча­стоте k собственных колебаний.

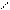
Подбирая различ­ные соотношения между р и k, можно получить вынужденные коле­бания с разными амплитудами. При p=0 амплитуда равна δ₀ (или близка к этой величине). Если величина р близка к k, амплитуда A становится очень большой. Когда p k, амплитуда A становится очень малой (практически близка к нулю).

Резонанс. В случае, когда р = k, т. е. когда частота

возму­щающей силы равна частоте собственных

колебаний, имеет место так называемое явление

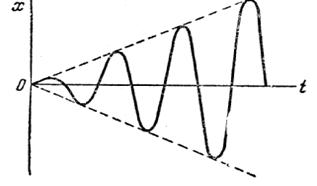
резонанса. Размахи вынужденных колебаний при

резонансе будут со временем неограниченно

возрастать так, как показано на рис. 17.

Рисунок 17

Дата добавления: 2014-12-17