Кинематика точки. Изучение данных вопросов необходимо в дальнейшем для динамики движения материальной точки, динамики относительного движения точки

Изучение данных вопросов необходимо в дальнейшем для динамики движения материальной точки, динамики относительного движения точки, динамики вращательного движения точки, для решения задач в дисциплинах «Теория машин и механизмов» и «Детали машин».

Санкт-Петербург, Межевой канал, 2.

Отпечатано в типографии ФГОУ ВПО СПГУВК,

СОПРОТИВЛЕНИЕ МАТЕРИАЛОВ

Методические указания к расчетно-графическим работам

Печатается в авторской редакции

Подписано в печать Сдано в производство

Форм. бум. 60х84 1/16 Офсетная печать

Усл.- печ. л. Усл.- изд. л.

Тираж экз. Зак. №

Санкт-Петербургский государственный университет водных коммуникаций

198035,Санкт-Петербург, ул. Двинская, 5/7

Кинематика точки и твердого тела

Введение в кинематику

Кинематикой называется раздел механики, в котором изучаются геометрические свойства движения тел без учета их инертности (массы) и действующих на них сил.

Под движением мы понимаем в механике изменение, с течением времени положения данного тела в пространстве по отношению к другим телам.

Для определения положения движущегося тела (или точки) в разные моменты времени с телом, по отношению к которому изучается движение, жестко связывают какую-нибудь систему координат, образующую вместе с этим телом систему отсчета.

Изображать систему отсчета будем в виде трех координатных осей (не показывая тело, с которым они связаны).

Движение тел совершается в пространстве с течением времени. Пространство в механике мы рассматриваем, как трехмерное евклидово пространство.

Время является скалярной, непрерывно изменяющейся величиной. В задачах кинематики время t принимают за независимое переменное (аргумент). Все другие переменные величины (расстояния, скорости и т. д.) рассматриваются как изменяющиеся с течением времени, т, е. как функции времени t.

Для решения задач кинематики надо, чтобы изучаемое движение было как-то задано (описано).

Кинематически задать движение или закон движения тела (точки) - значит задать положение этого тела (точки) относительно данной системы отсчета в любой момент времени.

Основная задача кинематики точки и твердого тела состоит в том, чтобы, зная закон движения точки (тела), установить методы определения всех кинематических величин, характеризующих дан­ное движение.

СПОСОБЫ ЗАДАНИЯ ДВИЖЕНИЯ ТОЧКИ

Для задания движения точки можно применять один из следую­щих трех способов:

1) векторный, 2) координатный, 3) естественный.

1. Векторный способ задания движения точки.

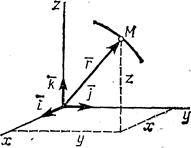
Пусть точка М движется по отношению к некоторой си­стеме отсчета Oxyz. Положение этой точки в любой момент времени можно определить, задав ее радиус-вектор r, проведенный из на­чала координат О в точку М (рис. 1).

При движении точки М вектор будет с течением времени изме­няться и по модулю, и по направлению. Следовательно, является переменным вектором (вектором-функцией), зависящим от аргу­мента t:.

.

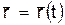Равенство определяет закон движения точки в векторной форме, так как оно позволяет в любой момент времени построить соответствующий вектор и найти положение движущейся точки.

Геометрическое место концов вектора , т. е. годограф этого вектора, определяет траекторию движущейся точки.

2. Координатный способ задания движе­ния точки.

Положение точки можно непосредственно опре­делять ее декартовыми координатами х, у, z, которые при движении точки будут с течением времени изменяться. Чтобы знать закон дви­жения точки, т. е. ее положение в пространстве в любой момент вре­мени, надо знать значения координат точки для каждого момента времени, т. е. знать зависимости

.

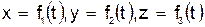4 Рис.1

Уравнения представляют собой уравнения движения точки в прямоугольных декартовых координатах. Они определяют закон движения точки при координатном способе задания движения.

3. Естественный способ задания движе­ния точки.

Естественным способом задания движения удобно пользоваться в тех слу­чаях, когда траектория движущейся точки известна заранее. Пусть кривая АВ явля­ется траекторией точки М при ее движении относительно системы отсчета Oxyz (рис, 2) Выберем на этой траектории какую-нибудь неподвижную точку О', которую примем за начало отсчета, и установим на траектории положительное и

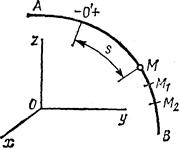отрицатель­ное направления отсчета (как на координат­ной оси).

Тогда положение точки М на тра­ектории будет однозначно

определяться криволинейной коорди­натой s, которая равна

расстоянию от точки О' до точки М, изме­ренному вдоль дуги

траектории и взятому с соответствующим знаком. При движении

точка М перемещается в положения M₁, М₂,... следовательно,

расстояние s будет с течением времени изменяться.

Чтобы знать положение точки М на траектории в любой Рис.2

момент времени, надо знать зависимость

.

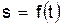Уравнение выражает закон движения точки М вдоль тра­ектории.

ВЕКТОР СКОРОСТИ ТОЧКИ

Одной из основных кинематических характеристик движе­ния точки является векторная величина, называемая скоростью точки. Введем сначала понятие о средней скорости точки за какой-нибудь промежуток времени. Пусть движущаяся точка находится

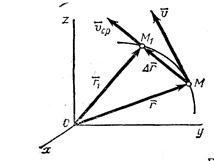
Рис.3

в момент времени t в положении М, определяемом радиусом-векто­ром r, а в момент t₁ приходит в положение M₁ определяемое векто­ром 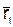(рис.3). Тогда перемещение точки за промежуток времени 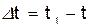определяется вектором 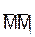который будем называть вектором перемещения точки. Из треугольника ОММ₁ видно, что 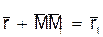; следовательно, .

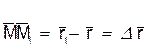Отношение вектора перемещения точки к соответствующему промежутку времени дает векторную величину, называемую сред­ней по модулю и направлению скоростью точки за промежуток времени .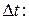

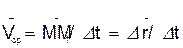Скоростью точки в данный момент времени t называется векторная величина v, к которой стремится средняя скорость v_ср при стремлении промежутка времени 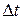к нулю:

, .

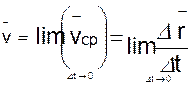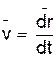Итак, вектор скорости точки в данный момент времени равен первой производной от радиуса-вектора точки по времени.

Так как предельным направлением секущей ММ₁ является касательная, то вектор скорости точки в данный момент времени направлен по касательной к траектории точки в сторону движения.

Вектор ускорения точки

Ускорением точки называется векторная величина,

характеризующая изменение с течением времени модуля и

направления скорости точки.

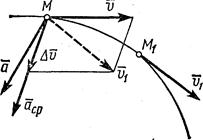
Пусть в некоторый момент времени t движущаяся

точка находится в положении М и имеет скорость v, а

в момент t₁ приходит в положение M₁ и имеет скорость Рис.4

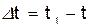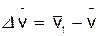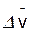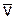v₁ (рис. 4). Тогда за промежуток времени скорость точки получает приращение . Для построения вектора отложим от точки М вектор, равный v₁, и построим параллелограмм, в котором диагональю будет , a одной из сторон . Тогда, очевидно, вторая сторона и будет изображать вектор 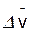. Заметим, что вектор 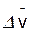всегда направлен в сторону вог­нутости траектории.

Отношение приращения вектора скорости 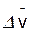к соответствующему про­межутку времени 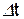определяет век­тор среднего ускорения точки за этот промежуток времени:

.

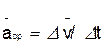Вектор среднего ускорения имеет то же направление, что и век­тор 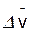, т. е. направлен в сторону вогнутости траектории.

Ускорением точки в данный момент времени t называется век­торная величина 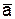, к которой стремится среднее ускорение 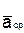при стремлении промежутка времени 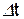к нулю: Вектор ускорения точки в данный момент време­ни равен первой производной от вектора скорости или второй произ­водной от радиуса-вектора точки по времени.

Найдем, как располагается вектор 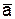по отношению к траекто­рии точки. При прямолинейном движении вектор 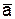направлен вдоль прямой, по которой движется точка. Если траекторией точки явля­ется плоская кривая, то вектор ускорения 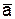, так же как и вектор 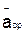, лежит в плоскости этой кривой и направлен в сторону ее вогнутости. Если траектория не является плоской кривой, то вектор 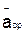на­правлен в сторону вогнутости траектории и лежит в плоскости, про­ходящей через касательную к траектории в точке М и прямую, па­раллельную касательной в соседней точке M₁ (рис. 4). В пределе, когда точка М стремится к М, эта плоскость занимает положение так называемойсоприкасающейся плоскости, т.е. плоскости, в которой происходит бесконечно малый поворот касательной к траектории при элементарном перемещении движущейся точки. Следовательно, в общем случае вектор ускорения 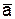лежит в соприкасающейся плоскости и направлен в сторону вогнутости кривой.

Определение скорости и ускорения точки при координатном способе задания движения

1. Определение скорости точки. Вектор скорости точки 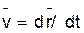, учитывая, что 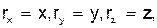найдем:

.

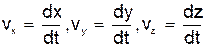Таким образом, проекции скорости точки на координатные оси равны первым производным от соответствующих координат точки по времени.

Зная проекции скорости, найдем ее модуль и направление (т.е. углы 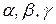, которые вектор v образует с координатными осями) по формулам

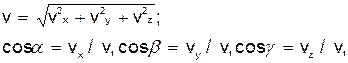
2. Определение ускорения точки. Вектор ускорения точки 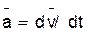в проекции на оси получаем:

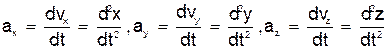
или

,

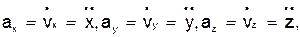т.е. проекция ускорения точки на координатные оси равны первым производным от проекций скорости или вторым производным от соответствующих координат точки по времени. Модуль и направление ускорения найдутся из формул

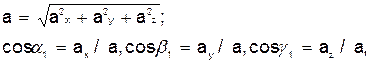
где 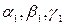- углы, образуемые вектором ускорения с координатными осями.

Итак, численная величина скорости точки в данный момент времени равна первой производной от расстояния (криволинейной координаты) s точки по времени.

Направлен вектор скорости по касательной к траектории, кото­рая нам наперед известна.

Касательное и нормальное ускорение точки

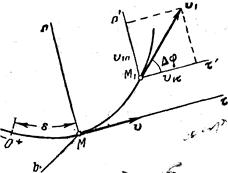
При естественном способе задания движения вектор 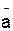определяют по его проекциям на оси M 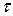nb, имеющие начало в точке М и движущиеся вместе с нею (рис.5). Эти оси, называемые осями естественного трехгранника (или скоростными осями), направлены следующим образом: ось - вдоль каса­тельной к траектории в сторону положительного отсчета расстояния s; ось М_n - по нормали, лежащей в соприкасающейся плос­кости и направленной в сторону вогнутости траектории; ось Mb - перпендикулярно к первым двум так, чтобы она образовала с ними правую тройку. Нормаль М_n, лежащая в соприкасающейся плоскости(вплоскости самой кривой, если кривая плоская), называетсяглавной нормалью, а перпендикулярная к ней нормаль Mb - бинормалью.

Было показано, что ускорение точки 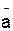лежит в соприкасающейся плоскости, т. е. в плоскости 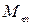; следовательно, проекция вектора 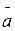на бинормаль равна нулю ().

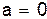Вычислим проекции 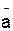, на две другие оси. Пусть в моментвремени t точка находится в положении М и имеет скоростьv, a в момент 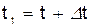приходит в положение М₁ и имеет скорость v₁.

Тогда по определению

Дата добавления: 2014-12-17