Цилиндрические зубчатые передачи

Рассмотрим основные виды этих передач.

1. Рядовой назовем передачу, в которой все оси колес, находящихся в по­следовательном зацеплении, неподвижны. При этом одно из колес (например, ко­лесо 1 на рис.31) является ведущим, а остальные ведомыми.

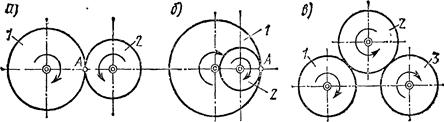
Рис.31

В случае внешнего (рис. 31, а) или внутреннего (рис. 31, б) зацепления двух колес имеем 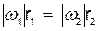, так как скорость точки сцепления А у обоих колес одинакова. Учитывая, что число z зубцов сцепленных колес пропорционально их радиусам, а вращения колес происходят при внутреннем зацеплении в одну сторону, а при внешнем в разные, получаем

.

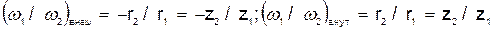При внешнем зацеплении трех колес (рис. 32, в) найдем, что

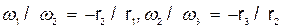и .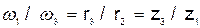

Следовательно, отношение угловых скоростей крайних шестерен в этой пере­даче обратно пропорционально их радиусам (числу зубцов) и не зависит от радиу­сов промежуточных (паразитных) шестерен.

Из полученных результатов следует, что при рядовом сцеплении шестерен

.

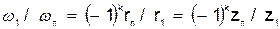где k - число внешних зацеплений (в случае, изображенном на рис.31,а имеется одно внешнее зацепление; на рис.31, в - два внешних зацепления, на рис.31, б внешних зацеплений нет).

Передаточным числом данной зубчатой передачи называется величина 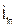, дающая отношение угловой скорости ведущего колеса к угловой скорости ведомого:

.

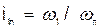2. Планетарной называется передача (рис.32), в которой шестерня 1 неподвижна, а оси остальных шестерен, находящихся в последовательном зацеп­лении, укреплены на кривошипе АВ, вращающемся вокруг оси неподвижной шестерни.

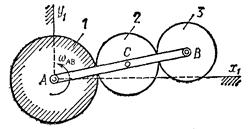
Рис.32

3. Дифференциальной называется передача, изображенная на рис. 32, если в ней шестерня 1 не является неподвижной и может вращаться вокруг своей оси А независимо от кривошипа АВ.

Расчет планетарных и дифференциальных передач можно производить, со­общив мысленно всей неподвижной плоскости Ах₁y₁ вращение с угловой скоростью - _AB, равной по модулю и противополож­ной по направлению угловой скорости кривошипа АВ (метод остановки или ме­тод Виллиса).

Тогда кривошип в этом сложном движении бу­дет неподвижен, а любая шестерня радиуса r_k будет иметь угловую скорость

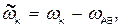
где _k - абсолютная угловая скорость этой шестерни по отношению к осям Ах₁y₁ (рис.32). При этом оси всех шестерен будут неподвижны и зависимость между 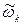можно будет определить приравнивая скорости точек сцепления.

Расчет планетарных и дифференциальных передач можно также производить с помощью мгновенных центров скоростей.

Сложение поступательного и вращательного движений. Винтовое движение.

Если сложное движение тела слагается из вращательного вокруг оси Аа с угловой скоростью 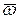и поступательного со скоростью v, направленной параллельно оси Аа (рис.33), то такое движение тела называется винтовым. Ось Аа называют осью винта. Когда векторы v и 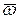направлены в одну сторону, то при принятом нами правиле изображения винт будет правым; если в разные стороны, - левым.

Расстояние, проходимое за время одного оборота любой точкой тела, лежащей на оси винта, называется шагом h винта. Если величи­ны v и 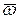постоянны, то шаг винта также будет постоянным. Обо­значая время одного оборота через Т, получаем в этом случае vT=h и T=2 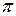, откуда h=2 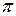v/ .

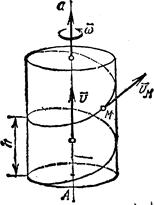
Рис.33

При постоянном шаге любая точка М тела, не лежащая на оси винта, описывает винтовую линию. Скорость точки М, находящей­ся от оси винта на расстоянии r, слагается из поступательной ско­рости v и перпендикулярной ей скорости, получаемой во враща­тельном движении, которая численно равна 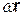. Следовательно,

.

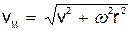Направлена скорость по касательной к винтовой линии. Если цилиндрическую поверхность, по которой движется точка М, разрезать вдоль образующей и развернуть, то винтовые линии, обратятся в прямые, наклоненные к основанию цилиндра под углом .

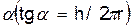Рекомендуемая литература

1. Яблонский А.А. Курс теоретической механики. Т. 1,2. - М.: Высш. шк., 1977.

2. Добронравов В.В., Никитин Н.Н. Курс теоретической механики. - М.,1980.

3. Тарг С.М. Краткий курс теоретической механики. - М.: Высш. шк., 1986.

4. Лойцянский Л.Г., Лурье А.И. Курс теоретической механики. Т.1,2. - М., 1982.

Дата добавления: 2014-12-17