Теорема Коші (про існування і єдиність розв’язку)

Нехай функція і її частинна похідна визначені і неперервні у відкритій області площини і точка 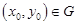. Тоді існує єдиний розв’язок 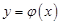рівняння (2), який задовольняє умову

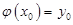при , тобто . (4)

Ця теорема дає достатні умови існування єдиного розв’язку рівняння (2).

Умову (4) згідно з якою розв’язок 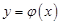набуває наперед задане значення 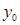в заданій точці , називають початковою умовою розв’язку і записують так:

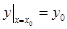або . (5)

Задача знаходження розв’язку рівняння (2), який задовольняє початкову умову (5), називається задачею Коші. З погляду геометрії розв’язати задачу Коші – це означає виділити з множини інтегральних кривих ту, яка проходить через задану точку .

Точки площини, в яких не виконуються умови теореми Коші, називаються особливими. Через кожну з таких точок проходить кілька інтегральних кривих або не проходить жодної.

Розв’язок диференціального рівняння, в кожній точці якого порушується умова єдиності, називають особливим розв’язком. Графік особливого розв’язку називають особливою інтегральною кривою.

Нехай права частина диференціального рівняння (2) задовольняє в області умови теореми Коші.

Функція 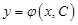, яка залежить від аргументу 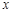і довільної сталої 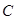, називається загальним розв’язком рівняння (2) в області , якщо вона задовольняє дві умови:

1) функція 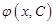є розв’язком рівняння при будь-якому значенні сталої 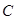з деякої множини;

2) для довільної точки 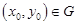можна знайти таке значення , що функція задовольняє початкову умову .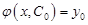

Частинним розв’язком рівняння (2) називається функція , яка утворюється із загального розв’язку 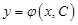при певному значенні сталої .

Якщо загальний розв’язок диференціального рівняння знайдено в неявному вигляді, тобто у вигляді рівняння , то такий розв’язок називають загальним інтегралом диференціального рівняння. Рівність 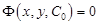у цьому випадку називають частинним інтегралом рівняння.

Приклад 1.1. Довести, що при будь-якому 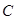функція є розв’язком рівняння . Знайти частинний розв’язок, що задовольняє початкову умову .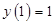

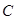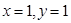Значить дана функція є розв’язком рівняння при будь-якому значенні . Підставимо у функцію початкові умови , знайдемо , тобто . Таким чином, шуканим частинним розв’язком є функція .

Дата добавления: 2014-12-17