
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Обратные матрицы. Математическая часть
|
|
|
|
Пусть А и С – квадратные матрицы порядка  . Решить матричное уравнение
. Решить матричное уравнение
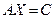 , (2.1)
, (2.1)
это значит найти такую квадратную матрицу В, что АВ=С. При этом В называется решением матричного уравнения (2.1).
Непосредственно из определения операции умножения матриц вытекает следующее утверждение.
Утверждение 2.1. Матрица В является решением матричного уравнений (2.1), если и только если ее столбцы 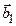 ,
, 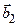 , …
, … 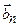 являются соответственно решениями
являются соответственно решениями  систем линейных уравнений
систем линейных уравнений 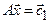 ,
, 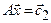 , …,
, …, 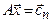 , где
, где 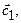
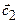 , …,
, …, 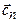 - столбцы матрицы С,
- столбцы матрицы С, 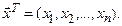
Матричному уравнению (2.1) можно поставить в соответствие расширенную матрицу К=(АС) размера 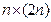 , приписав справа к матрице А матрицу С. В то же время любой матрице К размера
, приписав справа к матрице А матрицу С. В то же время любой матрице К размера 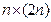 можно однозначно сопоставить матричное уравнение вида (2.1), положив, что первые
можно однозначно сопоставить матричное уравнение вида (2.1), положив, что первые  столбцов в К составляют матрицу А, последние
столбцов в К составляют матрицу А, последние  столбцов – матрицу С. В этих случаях матрицу К и матричное уравнение (2.1) будем называть соответствующими.
столбцов – матрицу С. В этих случаях матрицу К и матричное уравнение (2.1) будем называть соответствующими.
Утверждение 2.1 фактически доказано при доказательстве теоремы 2.1.
Из утверждений 2.1 и 1.2 вытекает следующее утверждение.
Утверждение 2.2. Элементарные преобразования расширенных матриц не изменяют множеств решений соответствующих матричных уравнений.
Теорема 2.1. Пусть в уравнении (2.1) матрица С является единичной, т.е. С=Е. Тогда уравнение (2.1) имеет решение, если и только если матрица А невырожденная.
Доказательство. Согласно следствию 1. 6 существует такая последовательность 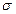 элементарных преобразований строк матрицы А, которая приводит матрицу А к единичной матрице того же порядка в случае невырожденности А, либо к некоторой матрице
элементарных преобразований строк матрицы А, которая приводит матрицу А к единичной матрице того же порядка в случае невырожденности А, либо к некоторой матрице 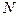 того же порядка, содержащей хотя бы одну нулевую строку, в случае вырожденности А. Применим последовательность
того же порядка, содержащей хотя бы одну нулевую строку, в случае вырожденности А. Применим последовательность 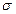 к строкам расширенной матрицы АЕ. После того как «левая половина» этой матрицы приведется к Е, правая приведется к некоторой матрице
к строкам расширенной матрицы АЕ. После того как «левая половина» этой матрицы приведется к Е, правая приведется к некоторой матрице  . В силу утверждения 2.2 пары матричных уравнений
. В силу утверждения 2.2 пары матричных уравнений 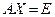 и
и 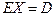 (или
(или 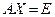 и
и 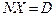 ) имеют одинаковые множества решений. Рассмотрим первую пару. Очевидно, решением уравнения
) имеют одинаковые множества решений. Рассмотрим первую пару. Очевидно, решением уравнения 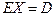 является матрица
является матрица  (см. теорему 1.12) и, следовательно,
(см. теорему 1.12) и, следовательно,  является решением уравнения
является решением уравнения 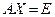 . Рассмотрим вторую пару. Предположим, что в
. Рассмотрим вторую пару. Предположим, что в 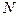
 -я строка нулевая. Тогда в произведении
-я строка нулевая. Тогда в произведении 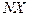
 -я строка также будет нулевой, что невозможно, ибо
-я строка также будет нулевой, что невозможно, ибо 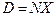 , а матрица
, а матрица  получена из невырожденной матрицы Е элементарными преобразованиями и потому в силу теоремы 1.8 не может содержать нулевых строк. Теорема доказана.
получена из невырожденной матрицы Е элементарными преобразованиями и потому в силу теоремы 1.8 не может содержать нулевых строк. Теорема доказана.
Следствие 2.1. Пусть А и Е – квадратные матрицы одного порядка. Если матричное уравнение
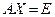 (2.2)
(2.2)
имеет решение, то оно единственное.
Определение. Обратной матрицей для матрицы А называется решение матричного уравнения (2.2). Обратная для А матрица обозначается 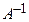 .
.
Следствие 2.2. Невырожденные матрицы, и только они, имеют обратные.
Следствие 2.3. Матрица, обратная для 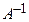 , есть А, т.е.
, есть А, т.е. 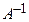
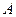 =
= 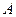
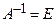 .
.
Доказательство. Если применить в обратном порядке последовательность элементарных преобразований 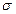 (см. доказательство теоремы 2.1) к строкам матрицы
(см. доказательство теоремы 2.1) к строкам матрицы 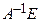 , то получим матрицу
, то получим матрицу 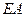 , откуда следует, что А является обратной для
, откуда следует, что А является обратной для 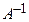 (см. далее приведенное практическое правило построения обратной матрицы).
(см. далее приведенное практическое правило построения обратной матрицы).
Следствие 2.4. Пусть 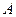 - невырожденная матрица. Тогда единственным решением матричного уравнений (2.1) является
- невырожденная матрица. Тогда единственным решением матричного уравнений (2.1) является 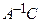 .
.
Доказательство. 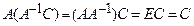 (см. теорему 2.1), откуда
(см. теорему 2.1), откуда 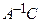 - решение матричного уравнения (2.1). Предположим теперь, что имеется еще одна матрица
- решение матричного уравнения (2.1). Предположим теперь, что имеется еще одна матрица 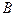 такая, что
такая, что 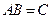 . Умножим обе части этого равенства слева на матрицу
. Умножим обе части этого равенства слева на матрицу 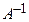 (такая матрица существует в силу следствия 2.1):
(такая матрица существует в силу следствия 2.1):
 или
или 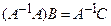 , или
, или 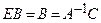 .
.
Следствие 2.5. Пусть 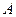 - невырожденная матрица порядка
- невырожденная матрица порядка  . Тогда для любого вектора-столбца
. Тогда для любого вектора-столбца 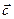 размерности
размерности  система уравнений
система уравнений 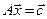 имеет единственное решение
имеет единственное решение 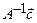 .
.
Доказательство аналогично предыдущему.
Из доказательства теоремы 2.1 вытекает следующее практическое правило проверки матрицы на невырожденность и построения обратной матрицы: с помощью элементарных преобразований строк расширенной матрицы АЕ привести «левую половину» к единичной матрице (если в ходе этого процесса образуется хотя бы одна нулевая строка в этой «левой половине», то А вырожденная); тогда на место первоначально приписанной матрицы Е окажется матрица 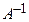 .
.
|
|
|
|
|
Дата добавления: 2014-11-29; Просмотров: 517; Нарушение авторских прав?; Мы поможем в написании вашей работы!