Определители. Задачи

Пример.

Следствие 2.6. Квадратная матрица А невырождена, если и только если ее определитель отличен от нуля.

Доказательство. Согласно следствию 1.6, с помощью элементарных преобразований строк матрицу А можно привести либо к единичной матрице в случае невырожденности А, либо к матрице, содержащей нулевую строку, в случае вырожденности А. В первом случае 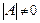в силу теоремы 2.2 и свойства 2.5, во втором случае

в силу свойства 2.1. Следствие доказано.

Определение. Матрица

называется присоединенной для квадратной матрицы А.

Следствие 2.7. Если , тио матрица 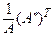является обратной для А.

Доказательство. Элемент матрицы на позиции равен . Но при 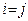эта сумма равна (теорема 2.1), а при эта сумма равна нудю (свойство 2.4). Поэтому

=

откуда , что доказывает следствие.

Если то ,

.

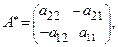
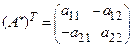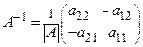1. Доказать свойства 2.1 и 2.5.
2. Вывести следующее правило «треугольника» для вычисления определителя матрицы третьего порядка:

.

1. Доказать, что
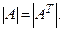
2. Квадратная матрица называется треугольной, если все ее элементы, находящиеся выше (ниже) главной диагонали, равны нулю. Доказать, что определитель треугольной матрицы равен произведению всех ее элементов на главной диагонали. В частности, .
3. Пусть даны функций 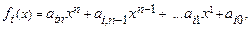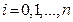. Доказать, что если все они одновременно обращаются в нуль при некотором значении , то определитель матрицы , -я строка которой совпадает с вектором-строкой равен нулю.
4. Квадратная матрица А называется кососимметрической, если все ее элементы на главной диагонали равны нулю, а сумма лбюых двух элементов, симметричных относительно главной диагонали, также равна нулю, т.е. 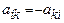. Доказать, что определитель кососимметрической матрицы нечетного порядка равен нулю.
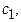
5. Пусть все числа 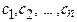различны. Тогда матрицей Вандермонда называется матрица:

Доказать, что определитель матрицы Вандермонда равен произведению всех разностей вида , где .

1. Пусть А – квадратная матрица порядка . Произведение называется членом определителя, если координаты вектора составлены из номеров столбцов (в произвольном порядке) матрицы А, а - число всех таких пар координат вектора 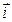, в которых большее число расположено в векторе 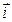раньше меньшего (такие пары называются инверсиями). Заметим, что член определителя матрицы А состоит из сомножителей, взятых ровно по одному из каждой строки и каждого столбца матрицы.

Доказать, что сумма всех членов определителя матрицы А порядка равна .

Дата добавления: 2014-11-29