Ответы, указания, решения

Задачи для самостоятельного решения

1. Найти вектор 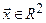, имеющий минимальный модуль ошибки среди других векторов пространства .

а) , ;

б) , ;

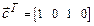в) , ;

г) , ;

д) .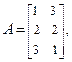

1 д). Решение. Матрица А элементарными преобразованиями столбцов приводится к следующему виду:

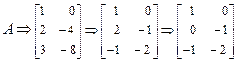
(вначале ко второму столбцу прибавляется первый, умноженный на -3; затем второй столбец умножается на : затем к первому столбцу прибавляется второй, умноженный на 2). Ясно, что в матрице 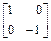столбцы линейно независимы (см. задачу 10 п. 1.3). Поэтому после добавления новой строки они таковыми и останутся (см. задачу 11 п.1.9). Следовательно, то же самое верно и для исходной матрицы А (задача 10 п. 1.3). Поэтому искомый вектор можно найти на основании теоремы 3.1:

.

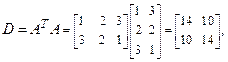
Обратную для матрицу найдем так же, как и в последнем примере п. 2.4:

Отсюда искомый вектор равен:

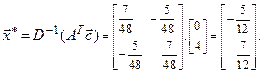
Глава 4. Собственные значения неотрицательных матриц

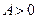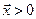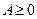Определение. Будем считать, что матрица или вектор положительны (неотрицательны), если все их элементы положительные (неотрицательные). Запись или ( или ) означает, что матрица А или вектор положительны (неотрицательны).

Определение. Число называется собственным значением квадратной матрицы А, если существует такой ненулевой вектор-столбец , для которого:

. (4.1)

Ненулевой вектор называется собственным вектором матрицы А, соответствующим собственному значению (нулевой вектор не считается собственным).

Определение. Пусть - некоторая переменная. - определитель квадратной матрицы . Уравнение называется характеристическим уравнением матрицы А.

Теорема 4.1. Число является собственным значением матрицы А, если и только если - корень ее характеристического уравнения.

Доказательство. Поскольку 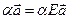, то условие (4.1) и 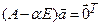эквивалентны. Число является собственным значением матрицы А, если и только если однородная система линейных уравнений 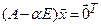имеет ненулевое решение. Из следствий 1.3 и 2.6 последнее равносильно равенству нулю определителя матрицы 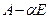. Теорема доказана.

Следствие 4.1. Множества собственных значений квадратных матриц 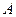и совпадают.

Для доказательства достаточно воспользоваться равенством .

Следующее утверждение приведем без доказательства.

Теорема 4.2 (теорема Перрона-Фробениуса). Квадратная неотрицательная матрица А имеет неотрицательное действительное собственное значение 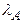, и модуль любого собственного значения матрицы А не превосходит 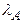( 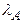называется максимальным собственным значением матрицы А) Среди собственных векторов, соответствующих 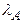, имеется неотрицательный вектор. Если А положительна, то 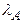превосходит модули всех других собственных значений матрицы А, и среди собственных векторов, соответствующих 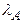, имеется положительный вектор.

Следствие 4.2. Если в квадратной неотрицательной матрице А сумма элементов каждого столбца равна 1, то максимальное собственное значение 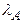матрицы А равно 1.

Доказательство. В силу теоремы 4.2 матрица А имеет неотрицательное собственное значение 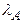, которому соответствует неотрицательный собственный вектор : . Если обозначить через 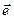вектор-строку, размерность которой равна порядку А, а все координаты равны 1, то условие о суммах элементов столбцов матрицы А можно записать в виде равенства . Умножив обе части этого равенства справа на вектор-столбец , получим

, , .

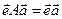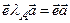Поскольку хотя бы одна координата вектора положительна, то число положительное. Поэтому 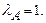Следствие доказано.

Определение. Неотрицательная квадратная матрица А порядка называется продуктивной, если для любого неотрицательного вектора-столбца 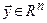существует неотрицательный вектор-столбец такой, что .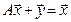

Теорема 4.3. Неотрицательная квадратная матрица А продуктивна, если и только если ее максимальное собственное значение 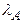меньше 1.

Доказательство. В силу теоремы 4.2 и следствия 4.1 матрицы 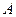и имеют неотрицательное собственное значение 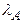, причем модули других их собственных значений не превосходят 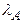, и значению 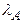соответствует такой неотрицательный вектор , что .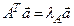

Предположим вначале, что матрица А порядка продуктивна. Тогда, в частности, для произвольного положительного вектора-столбца 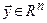найдется такой вектор-столбец из , что 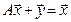. (Из этого равенства следует, что 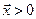). Умножим обе части этого равенства скалярно на вектор : 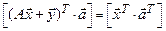, откуда по теореме 1.1 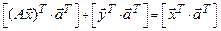. Но (см. теорему 1.14)

.

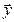Следовательно, . Согласно выбору, - положительный вектор, - неотрицательный ненулевой вектор, поэтому 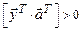. По той же причине . Следовательно, .

Положим теперь обратное, что . Покажем, что для произвольного неотрицательного вектора-столбца 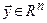найдется вектор-столбец 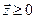такой, что . Для этого рассмотри матрицу , где . Тогда

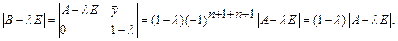
Отсюда по теореме 4.1 множество собственных значений матрицы В состоит из 1 и множества собственных значений матрицы А. Но по условию , поэтому .- максимальное собственное значение матрицы В. Этому значению в силу теоремы 4.2 соответствует неотрицательный собственный вектор и . Обозначим через вектор . Тогда , откуда 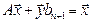. Если , то 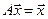и, следовательно, - собственное значение матрицы А, что противоречит предположению . 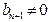Поэтому , и 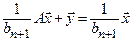. Последнее означает, что вектор - искомый. Теорема доказана.

Следствие 4.3. Неотрицательная квадратная матрица А порядка продуктивна, если и только если для матрицы существует обратная неотрицательная матрица.

Доказательство. Предположим вначале, что для существует обратная неотрицательная матрица 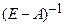. Для произвольного неотрицательного вектора 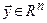обозначим через . Тогда 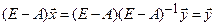или , причем из неотрицательности 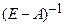следует, что . Таким образом матрица А продуктивная по определению.

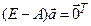Предположим теперь, что А – продуктивная матрица, но для матрицы не существует обратной. По следствию 2.2 это равносильно тому, что матрица вырождена. А это в свою очередь равносильно наличию ненулевого решения однородной системы ., т.е. . В этом случае - собственное значение матрицы А, однако по теореме 4.3 ее собственные значения меньше 1. Осталось предположить, что А – продуктивная матрица, но для матрицы существует обратная матрица, среди элементов которой встречаются отрицательные. Пусть - один из них., а 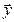- вектор-столбец из , -я координата которого равна 1, а остальные координаты равны нулю. Тогда ввиду продуктивности А существует неотрицательный вектор-столбец такой, что 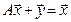. Отсюда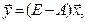 . Но -я координата в равна , что противоречит неравенству . Следствие доказано.

Дата добавления: 2014-11-29