Ответы, указания, решения. Общий алгоритм решения задач 1 а)-в)

Общий алгоритм решения задач 1 а)-в)

Ввести матрицу А коэффициентов прямых затрат, вектор y конечной продукции, вектор норм прибавочной стоимости, а также векторы возможного процентного изменения конечной продукции и норм прибавочной стоимости . На основе теоремы 4.3 установить продуктивность матрицы А:

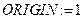
В случае утвердительного ответа на основе теоремы 5.1 определить ее запас продуктивности

. Найдя суммы элементов всех столбцов матрицы А, определить рентабельные и нерентабельные отрасли:

Определить вектор валового выпуска продукции 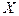и спрогнозировать цены на продукцию каждой отрасли (вектор ):

.

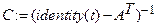
Найти возможные процентные изменения валового выпуска и цен:

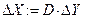
1 а). Ответы: валовый выпуск равен ; прогнозируемые цены равны

1 б). Ответы: матрица не продуктивна.

1в). Ответы: запас продуктивности равен 1.0065.

Глава 6. Модели международной торговли

Основу линейной модели международной торговли составляет структурная матрица торговли А, порядок которой равен числу стран-участниц, а на позиции 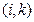находится элемент , равный части торгового бюджета -й страны, идущего на импорт товаров из -й страны. Предполагается также, что каждая страна расходует весь свой торговый бюджет на закупку товаров внутри страны и на импорт из других стран, причем А>0. Очевидно, сумма элементов каждого столбца матрицы А равна1, а выручка -й страны от торговли составит , где - торговый бюджет -й страны.

Определение. Сбалансированность торговли (или бездефицитность торгового бюджета) означает выполнимость неравенств:

(6.1)

Лемма 6.1. Система неравенств (6.1) равносильна системе равенств:

(6.2)

Доказательство. Предположим, что хотя бы одно из неравенств в (6.1) строгое. Тогда, сложив их все почленно, получим:

(6.3)

Но

,

Что противоречит (6.2). Лемма доказана.

Теорема 6.1. Всегда существует положительный вектор торговых бюджетов стран-участниц, обеспечивающий сбалансированность торговли. При этом любой другой такой вектор может быть получен из умножением на некоторое положительное число.

Доказательство. Сбалансированность торговли означает существование такого положительного вектора , при котором (лемма 6.1). Но по следствию 4.2 и теореме 4.2 матрица А имеет максимальное собственное значение 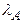, равное 1, и ему соответствует некоторый положительный собственный вектор , причем любой друцгой положительный собственный вектор матрицы А имеет вид , где - произвольное положительное число (см. задачу 7 п.4.1). Теорема доказана.

Теорема 6.1. означает возможность задать такие соотношения торговых бюджетов стран-участниц, при которых будет обеспечена сбалансированность торговли.

Дата добавления: 2014-11-29