Ответы, указания, решения. 2. Указание:воспользоваться теоремой 2.1 и примером в начале пункта 2.4

2. Указание: воспользоваться теоремой 2.1 и примером в начале пункта 2.4.

3. Решение. Докажем индукцией относительно порядка матриц. Утверждение непосредственно проверяется при 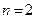. Предположим, что оно верно для всех квадратных матриц порядка . Докажем его справедливость для произвольной матрицы А порядка . Обозначим 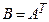и разложим 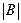по первому столбцу:

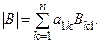Но 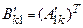и, следовательно, по индуктивному предположению . Поэтому

.

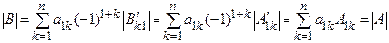4. Решение. Докажем индукцией относительно порядка матриц. Утверждение непосредственно проверяется для треугольных квадратных матриц порядка 2. Предположим, что оно верно для всех квадратных треугольных матриц порядка . Докажем его справедливость для произвольной треугольной матрицы А порядка . Для определенности считаем, что все элементы матрицы А, которые выше главной диагонали, равны нулю. Разложим по первой строке:

где - треугольная матрица порядка и, следовательно, для нее выполняется индуктивное предположение, т.е. . Отсюда , что и требовалось доказать.

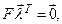5. Решение. Если обозначить через вектор-строку , то согласно условию, т.е. однородная система линейных уравнений имеет ненулевое решение 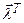. Поэтому по следствию 1.3 столбцы матрицы F линейно зависимы, т.е. F – вырожденная. Но тогда по следствию 2.6. Утверждение доказано.

6. Решение. Пусть

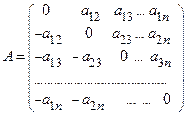
И нечетно. Если умножить каждую строку матрицы на -1, то опять получится матрица А. Из свойства 2.5 вытекает, что 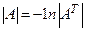или 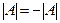, что возможно только при .

7. Решение. Докажем индукцией относительно порядка матрицы Вандермонда. Матрица Вандермонда второго порядка имеет вид и ее определитель равен , т.е. утверждение выполняется. Предположим, что утверждение верно для матриц Вандермонда порядка . Произведем следующие элементарные преобразования столбцов матрицы В: поочередно из каждого столбца, начиная с -го, вычитаем предыдущий столбец, умноженный на . В результате получим матрицу:

,

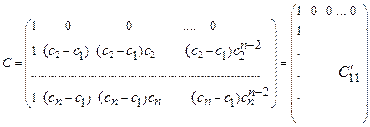откуда

.

Из того, что последний сомножитель является определителем матрицы Вандермонда порядка . Следует требуемое утверждение.

7. Доказательство. Доказательство утверждения проведем индукцией относительно порядка матрицы А. Для матриц второго порядка его справедливость проверяется непосредственно. Предположим, что утверждение верно для матрицы порядка и рассмотрим квадратную матрицу порядка . Из определения определителя следует, что

.

По индуктивному предположению для любой матрицы определитель состоит из 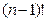слагаемых, каждое из которых содержит в качестве сомножителей ровно по одному элементу из каждой строки и каждого столбца матрицы . Поэтому рассматриваемая сумма может быть представлена в виде 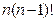слагаемых, составленных таким же образом. Осталось доказать, что каждое такое слагаемое фактически является членом определителя. Рассмотрим одно из таких слагаемых в выражении . По индуктивному предположению оно равно:

,

где 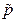- число инверсий вектора 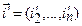, координаты которого составлены из номеров столбцов матрицы , содержащих соответственно элементы матрицы А. При этом следует отметить, что из-за исключения -го с толбца из матрицы А происходит сдвиг ее номеров столбцов (на 1 уменьшаются все номера с 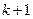-го по -1). Поэтому

(2.3)

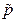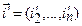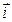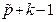Сравним числа и , где - число инверсий вектора Ввиду (2.3) число инверсий, образованных парами координат, не содержащих в векторах и одинаково. Число , стоящее на первом месте в векторе , образует инверсию с меньшими числами 1.2. …, . Поэтому Числа и имеют одинаковую четность. Следовательно, слагаемое 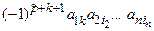равно члену определителя . Отсюда следует, что сумма членов определителя матрицы А равна .

Глава 3. Метод наименьших квадратов

Очевидно, система линейных уравнений 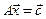не всегда имеет непустое множество решений. В связи с этим (и не только) возникает вопрос о существовании такого вектора , при котором левая часть 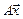минимально отличалась бы от правой части .

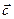Определение. Пусть даны матрица А размера 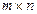, вектор-столбец 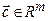и вектор-столбец . Тогда вектор называется ошибкой вектора и обозначается через 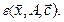Квадрат длины вектора будем называть модулем ошибки вектора .

Теорема 3.1. Пусть дана матрица А размерности 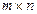с линейно независимыми столбцами и вектор- столбец 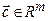. Тогда найдется единственный вектор-столбец , для которого модуль ошибки минимален, причем .

Доказательство. Предположим, что матрица 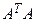вырождена. Тогда в силу следствия 1.3 однородная система линейных уравнений 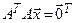имеет некоторое ненулевое решени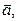е т.е. . Домножим обе части этого равенства слева на 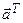, получим теперь воспользуемся теоремой 1.12, замечанием 1.1 и задачей и теоремой 1.14:

,

т.е. (см. задачу 1 в п. 1.3). А это возможно только в случае линейной зависимости столбцов матрицы (следствие 1.3).

Итак, доказана невырожденность матрицы 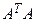. Но тогда для 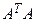найдется обратная матрица (следствие 2.2). Обозначим через вектор . Осталось доказать, что для любого вектора-столбца , не равного 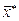, верно неравенство .

Обозначим через 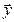. Тогда, применяя теорему 1.12, получаем:

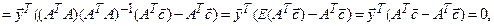
т.е. и ортогональны. Из равенства вытекает, что Используя теорему 1.1 и ортогональность векторов и , получаем:

Поскольку 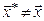, то может равняться нулю только в случае линейной зависимости столбцов матрицы А. Так как столбцы этой матрицы линейно независимы, то 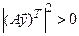. Отсюда следует последнее неравенство. Теорема доказана.

Дата добавления: 2014-11-29