Розкриття невизначеностей, І і ІІ визначні границі

ВСТУП В МАТЕМАТИЧНИЙ АНАЛІЗ

МОДУЛЬ 2

Обчислення границь базується на таких основних теоремах:

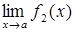· Якщо існують і , то:

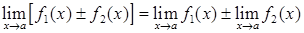, (2.1.1)

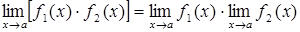, (2.1.2)

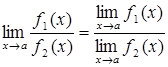
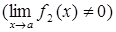, (2.1.3)

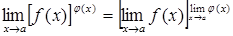. (2.1.4)

· Перша визначна границя:

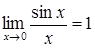. (2.1.5)

· Друга визначна границ я:

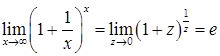. (2.1.6)

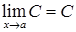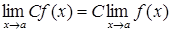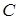· ; , ( ‑ стала величина). (2.1.7)

· Для всіх неперервних функцій

. (2.1.8)

· Слід пам'ятати, що (для ):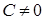

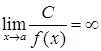, якщо 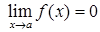; 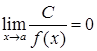, якщо .

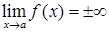Щодо техніки обчислення границь, слід відзначити, що в найпростіших випадках знаходження границі зводиться до підстановки у вираз під знаком границі граничного значення аргументу. Але часто така підстановка призводить до невизначених виразів виду 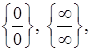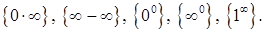Знаходження границь у цих випадках називається розкриттям невизначеності.

Наприлад, якщо невизначеність 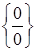з’явиться, коли в чисельнику (знаменнику) є ірраціональний вираз, тоді треба позбутися ірраціональність у чисельнику (знаменнику) шляхом помноження на "спряжений" вираз.

Невизначеність виду 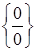при наявності тригонометричних функцій розкривається за допомогою першої визначної границі та часто вимагає попередніх тотожних перетворень (наприклад, за допомогою формул: , , , ).

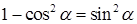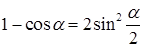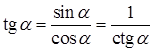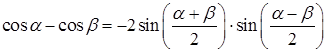Друга визначна границя розкриває невизначеність 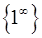. Наслідками (2.1.6) є вирази:

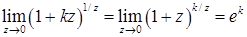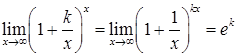, . (2.1.9)

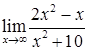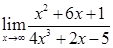Приклад 2.1.1. Знайти границі: 1) , 2) , 3) .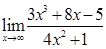

Розв’язання. 1) Маємо невизначеність 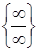. Винесемо в чисельнику і знаменнику старший ступінь змінної і скоротимо:

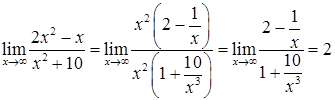(тому, що , ).

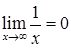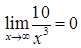Аналогічно,

2) ;

3) .

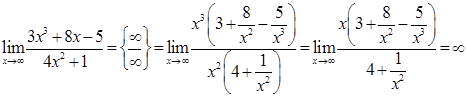Приклад 2.1.2. Обчислити .

Розв’язання. В даному випадку користуватися формулою (2.1.3) не можна, тому що границя знаменника дорівнює нулеві. Безпосередня же підстановка у вираз під знаком границі граничного значення аргументу приводить до невизначеності .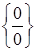

Розкладемо на множники чисельник і знаменник. (Зауважимо, що 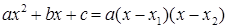, якщо 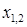‑ корені). Коренями квадратного рівняння 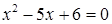є 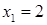, , 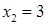значить .

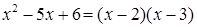Отже, за рахунок розкладання на множники і скорочення, позбавляємось невизначеності, після чого в результаті підстановки в отриманий вираз маємо

.

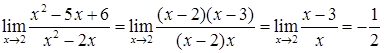Приклад 2.1.3. Обчислити 1) , 2) .

Розв’язання. 1) Підстановка у вираз (під знаком границі) 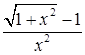значення приводить до невизначеності 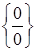. Для її розкриття помножимо чисельник і знаменник на вираз, що "спряжений" з чисельником (користуючись формулою скороченного множення 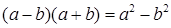). Після цього скоротимо на 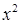і одержимо:

.

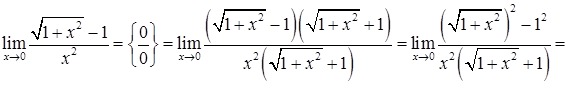
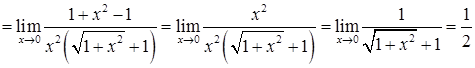2) У випадку маємо невизначеність 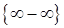. Помноження і ділення виразу під знаком границі на "спряжений" з ним вираз 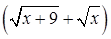з урахуванням (2.1.7)) дає:

.

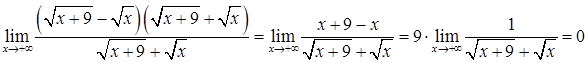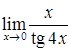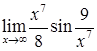Приклад 2.1.4. Знайти границі: 1) , 2) , 3) .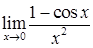

Розв’язання. Враховуючи, що 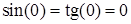, , 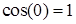за допомогою формул тригонометрії, властивості (2.1.2) та першої визначної (2.1.5) маємо:

1)

,

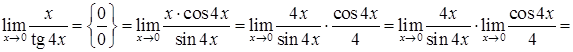
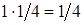2) ,

3) .

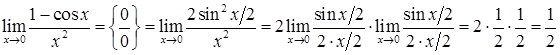Приклад 2.1.5. Знайти границі: 1) 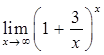, 2) .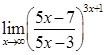

Розв’язання. Маємо невизначеність 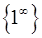, яка розкривається за допомогою другої визначної границі (2.1.6).

1)

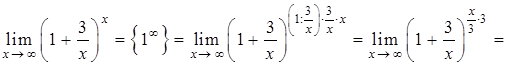
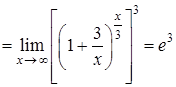(відповідь у данному випадку можна було отримати безпосередньо за (2.1.9)).

2)

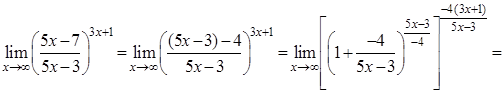
Зауважимо, що приклади 2.1.1 – 2.1.5 відповідають завданню 2.1 контрольної роботи.

Література: [1, с. 93 ‑ 125], [2, с. 101 ‑ 134], [3, с. 172 – 208, 247 ‑ 264], [7].

Дата добавления: 2014-12-17