
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Застосування похідних для дослідження функцій
Дослідження функцій методами диференціального числення можна проводити у відповідності з такою схемою:
1. Знаходження області визначення функції і точок розриву.
2. Визначення парності або непарності функції, її періодичності.
3. Визначення точок перетину графіком функції осей координат та інтервалів знакосталості функції.
4. Уточнення поведінки функції в околах точок розриву, та при 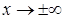 . Знаходження асимптот графіка функції.
. Знаходження асимптот графіка функції.
5. Визначення інтервалів монотонності, екстремумів функції.
6. Визначення інтервалів опуклості та угнутості, точок перегину.
7. Побудова графіка функції.
Зупинимося на деяких пунктах дослідження докладніше.
Пряманазивається асимптотою графіка функції, якщо відстань від точки  на графіці до цієї прямої прямує до нуля при віддаленні точки
на графіці до цієї прямої прямує до нуля при віддаленні точки  уздовж кривої в нескінченність. Розрізняють три види асимптот: вертикальні, горизонтальні, похилі. Якщо, то
уздовж кривої в нескінченність. Розрізняють три види асимптот: вертикальні, горизонтальні, похилі. Якщо, то  ‑ вертикальна асимптота (функція має розрив при
‑ вертикальна асимптота (функція має розрив при  ). Якщо (або), то пряма (або) є горизонтальною асимптотою. Похила асимптота має вигляд, де
). Якщо (або), то пряма (або) є горизонтальною асимптотою. Похила асимптота має вигляд, де
,, (2.3.1)
якщо зазначені границі існують.
Точки області визначення функції, в яких похідна дорівнює нулеві або не існує, називаються стаціонарними (критичними). Інтервал, на якому похідна від’ємна, є інтервалом спадання; інтервал, на якому похідна додатна, є інтервалом зростання. Знайдені стаціонарні точки потрібно нанести на числову пряму і встановити знак першої похідної зліва і справа від стаціонарної точки. Так визначають проміжки монотонності і наявність екстремуму функції. Екстремуми мають місце лише в тих критичних точках, де виконується достатня умова існування екстремума: якщо при переході через стаціонарну точку похідна змінює свій знак, то в стаціонарній точці є екстремум. Це максимум, якщо знак змінюється з плюса на мінус, і мінімум, якщо знак змінюється з мінуса на плюс.
Якщо друга похідна (тобто похідна від першої похідної) на інтервалі додатна, то графік функції угнутий, якщо друга похідна – від’ємна, то графік функції опуклий. Точки (де функція визначена), що розділяють інтервали опуклості й угнутості, називаються точками перегину. Друга похідна (якщо вона існує) в точці перегину дорівнює нулю.
Приклад 2.3.1. Знайти інтервали монотонності та екстремуми функції 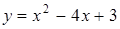 , а також інтервали опуклості і точки перегину.
, а також інтервали опуклості і точки перегину.
Розв’язання. Маємо 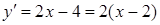 . Стаціонарна точка:
. Стаціонарна точка:  . Щоб знайти інтервали, де
. Щоб знайти інтервали, де  (або
(або 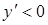 ) скористаємось методом інтервалів розв’язання нерівностей. Для цього нанесемо на вісь стаціонарні точки і (наприклад, за допомогою підстановки у
) скористаємось методом інтервалів розв’язання нерівностей. Для цього нанесемо на вісь стаціонарні точки і (наприклад, за допомогою підстановки у 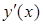 контрольних точок) з’ясуємо знак похідної на кожному інтервалі:
контрольних точок) з’ясуємо знак похідної на кожному інтервалі:
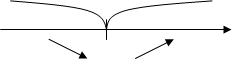
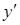
– +
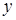 2
2 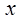
Рис. 2.3.1 – Знаки похідної за методом інтервалів
При 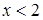 (контрольна точка
(контрольна точка 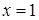 ,
, 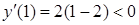 )
) 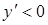 , а при
, а при 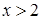 (контрольна точка
(контрольна точка 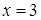 ,
,  )
) 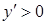 . Отже, функція
. Отже, функція 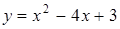 спадає на интервалі
спадає на интервалі 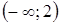 та зростає на интервалі
та зростає на интервалі 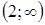 .
.
При переході через точку  знак похідної змінюється з “ - ” на “ + ”, отже
знак похідної змінюється з “ - ” на “ + ”, отже  ‑ точка мінімуму. При цьому
‑ точка мінімуму. При цьому  .
.
Знайдемо інтервали опуклості графіка функції: 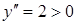 , отже фунція є угнутою при
, отже фунція є угнутою при  і не має точок перегину.
і не має точок перегину.
Приклад 2.3.2. Засобами диференціального числення дослідити функцію 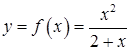 та побудувати її графік.
та побудувати її графік.
Розв’язання. 1. Область визначення функції: 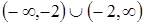 .
. 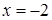 – точка розриву функції.
– точка розриву функції.
2. Функція – не парна (бо 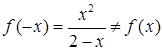 ) і не непарна (бо
) і не непарна (бо 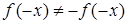 ). Функція – не періодична.
). Функція – не періодична.
3. Функція перетинає осі координат в точці 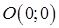 .
. 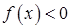 при
при 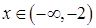 , і
, і 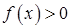 при
при 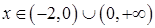 .
.
4. Оскільки 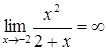 , то
, то 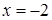 – вертикальна асимптота. Оскільки
– вертикальна асимптота. Оскільки  , то горизонтальної асимптоти немає. Знайдемо похилі асимптоти графіка функції:
, то горизонтальної асимптоти немає. Знайдемо похилі асимптоти графіка функції:
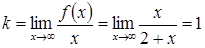 ;
; 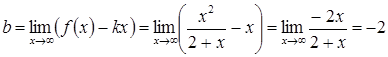 , таким чином,
, таким чином, 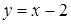 – похила асимптота.
– похила асимптота.
5. Знайдемо проміжки зростання, спадання і точки екстремуму.
Похідна (за (2.2.5)):
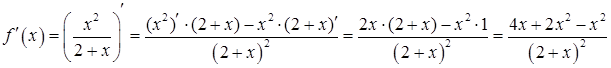
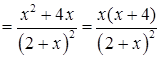 .
.
В точці 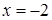 похідна функції не існує, а в точках
похідна функції не існує, а в точках 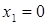 і
і 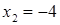 похідна
похідна 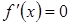 . Точки
. Точки 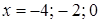 розбивають область визначення функції на інтервали
розбивають область визначення функції на інтервали 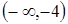 ,
, 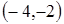 ,
, 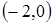 і
і 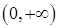 .
.
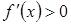 при
при 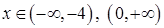 , значить функція зростає на цих інтервалах.
, значить функція зростає на цих інтервалах.
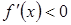 на інтервалах
на інтервалах 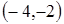 і
і 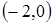 , значить функція спадає на цих інтервалах.
, значить функція спадає на цих інтервалах.
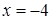 – точка максимуму і
– точка максимуму і 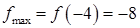 .
.
 – точка мінімуму і
– точка мінімуму і 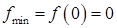 .
.
6. Знайдемо проміжки опуклості, угнутості і точки перегину.
Друга похідна: 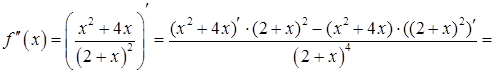
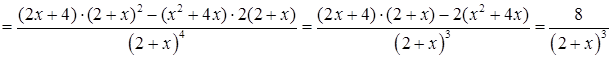 .
.
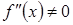 в усіх точках з області визначення функції. Точка розриву функції розбиває область визначення на два інтервали
в усіх точках з області визначення функції. Точка розриву функції розбиває область визначення на два інтервали 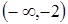 і
і 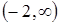 .
.
Якщо 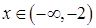 , то
, то 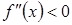 – графік функції є опуклим.
– графік функції є опуклим.
Якщо 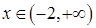 , то
, то 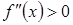 – графік функції є угнутим.
– графік функції є угнутим.
Точок перегину немає.
Всі дані заносимо в таблицю 2.3.1.
Таблиця 2.3.1 – Дослідження функції 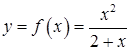
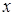
| 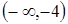
| 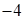
| 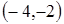
| 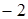
| 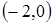
| 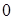
| 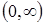
|
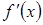
| + | – | не існує | – | + | ||
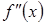
| – | – | – | не існує | + | + | + |
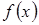
| < 0
 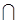
| = ‑ 8 max | < 0
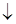 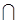
| не існує | > 0
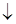 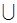
| = 0 min | > 0
 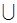
|
7. Побудуємо графік функції:
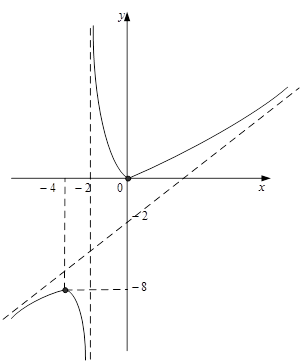
Рис. 2.3.2 – Графік функції 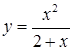
Зауважимо, що приклад 2.3.2 відповідає завданню 2.3 контрольної роботи.
Література: [1, с. 170 ‑ 196], [2, с. 191 ‑ 216], [3, с. 401 – 416], [9].
|
|
Дата добавления: 2014-12-17; Просмотров: 1322; Нарушение авторских прав?; Мы поможем в написании вашей работы!