Елементи векторної алгебри

Щоб знайти координативектора 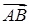, потрібно із координат його кінця відняти координати початку:

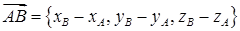. (1.2.1)

Довжина (модуль) вектора 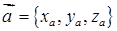дорівнює кореню квадратному із суми квадратів його координат:

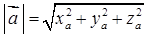. (1.2.2)

Ортом або одиничним вектором називається вектор, довжина якого дорівнює одиниці. Координатні орти:

.

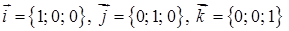При складанні (відніманні) векторів їхні координати складаються (віднімаються), а при множенні вектора на число його координати помножуються на це число.

Скалярним добутком 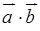векторів 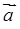і 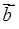називається число, що дорівнює добутку їхніх довжин на косинус кута між ними:

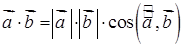. (1.2.3)

Якщо 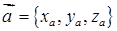, 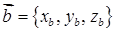тоді скалярний добуток

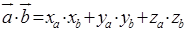. (1.2.4)

Якщо матеріальна точка (тіло) під дією постійної за величиною і напрямом сили 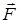переміщується уздовж вектора 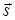, то робота сили обчислюється за формулою:

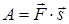. (1.2.5)

Векторний добуток 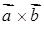– це вектор

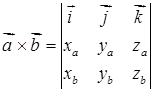. (1.2.6)

Якщо вектори 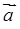і 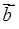мають спільний початок, то модуль векторного добутку дорівнює площі паралелограма, побудованого на цих векторах (обо подвоєній площі прямокутника).

Мішаним добутком 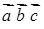трьох векторів 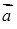, 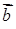і 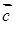називається їх векторно-скалярний добуток:

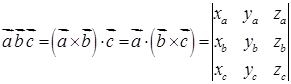. (1.2.7)

Якщо вектори 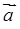, 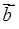і 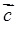мають спільний початок, то модуль мішаного добутку дорівнює об’ємові паралелепіпеда, побудованого на цих векторах (обо шести об’ємам піраміди).

У випадку

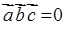, (1.2.8)

то вектори 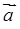, 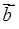і 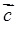є компланарними, тобто лежать в одній площині.

Вектори 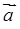, 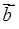є колінеарними (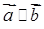), якщо

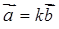, (1.2.9)

де 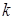‑ ненульове число.

Вектори 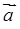, 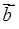є ортогональними (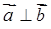), якщо

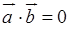. (1.2.10)

Приклад 1.2.1. За координатами вершин 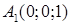, , 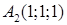, 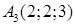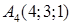піраміди 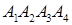знайти: а) довжину сторони 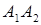, б) косинус кута між ребрами 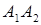і 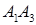, в) об’єм піраміди 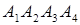, г) роботу рівнодіючої сил і 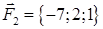, під дією якої тіло переміщується прямолінійно з точки 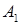в точку .

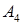Розв’язання. Знайдемо вектори 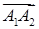, , 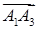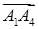за формулою (1.2.1): , , .

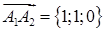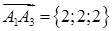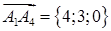а) Тоді за формулою (1.2.2) довжина сторони 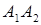дорівнює 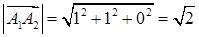(од.)

б) Згідно (1.2.3) та (1.2.4):

.

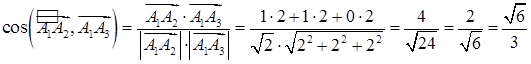в) Об’єм піраміди (шоста частина об’єма паралелепіпеда, побудованого на тих самих векторах) із застосуванням (1.2.7):

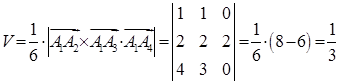(куб. од.),

г) Рівнодіюча сил і 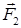‑ це сила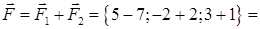 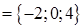, робота цієї сили згідно (1.2.5):

.

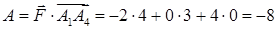Зауважимо, що приклад 1.2.1 відповідає завданню 1.2 контрольної роботи.

Література: [1, с. 296 ‑ 315], [2, с. 402 ‑ 432], [3, с. 12 – 22, 35 ‑ 63], [5], [6].

Дата добавления: 2014-12-17