
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Основные свойства пределов. Первый и второй замечательные пределы
|
|
|
|
Еще в школьном курсе математики были получены основные свойства пределов:
1. Предел постоянной величины x=с есть само число с.
Lim c = c.
2. Пусть x, y, …, z - конечное число переменных величин, каждая из которых имеет конечный предел. Тогда верны следующие утверждения:
а) их алгебраическая сумма (т.е. сумма или разность) также имеет предел u.
lim (x ± y ± … ± z) = limx ± limy ± … ± lim z;
б) их произведение также имеет предел
lim (x . y . … z) = limx . limy . … . limz.
3. Если существуют пределы переменных величин u и ф, причем limф≠0,
4. То существует предел частного этих переменных
lim  =
= 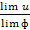
Доказательство этих свойств см.[1], стр. 43 – 44 (они носят название, соответственно, теоремы о предела суммы, разности, произведения и частного.). Все свойства пределов справедливы и для случая, когда в качестве переменных величин берутся функции. Свойства пределов облегчают их вычисление.
Рассмотрим несколько примеров.
Пример 1. Найди предел функции
y =  при x → 1
при x → 1
Решение. Воспользуемся свойствами пределов и найдем отдельно пределы числителя и знаменателя:
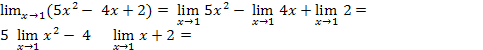 5 . 1 – 4 . 1 – 2 = 3
5 . 1 – 4 . 1 – 2 = 3
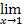 (3x2 + x – 3) =
(3x2 + x – 3) =  3x2 +
3x2 + 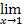 x -
x -  3 = 3. 1 + 1 – 3 = 1
3 = 3. 1 + 1 – 3 = 1
Применяя свойство 3, получим предел дроби:
y =  =
=  = 3
= 3
В этом примере непосредственное применение свойств пределов сразу привело нас к цели – мы получили конечный предел.
Однако на практике такие случаи встречаются крайне редко, а потому, прежде чем применять теоремы о пределах, приходится тождественно преобразовывать данную функцию. Покажем, как это делается на конкретных примерах.
Примеры вычисления предела функции.
1) limx→2(5x33-6x2+x-5)=5*23-6*22+2-5=5*8-24-3=40-27=13;
2) limx→2 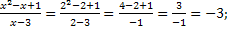
3) limx→2 
4) limx→0 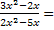 limx→0
limx→0  limx→0
limx→0 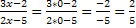
5)  8x3-1 разложим на множители по формуле a3-b3=(a-b)(a2+ab+b2)
8x3-1 разложим на множители по формуле a3-b3=(a-b)(a2+ab+b2)
4x2-1 по формуле a2-b2=(a-b)(a+b)
8x3-1=(2x-1)(4x2+2x+1);
4x2-1=(2x-1)(2x+1);




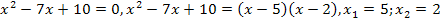


Глава 2 Производная
|
|
|
|
|
Дата добавления: 2014-12-17; Просмотров: 734; Нарушение авторских прав?; Мы поможем в написании вашей работы!