
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Правила дифференцирования
|
|
|
|
I. Примеры вычисления
Примеры
Пусть  . Тогда
. Тогда 
Пусть.  Тогда если
Тогда если  то
то 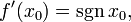
где 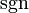 обозначает функцию знака. Если
обозначает функцию знака. Если  то
то  а следовательно
а следовательно  не существует.
не существует.
№1 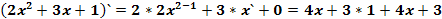
№2 
№3 
№4 
№5 
№6 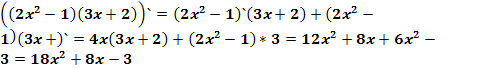
№7 
№8 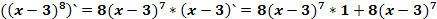
№9 
№10 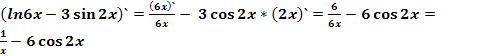
№11 
№12 

Операция нахождения производной называется дифференцированием. При выполнении этой операции часто приходится работать с частными, суммами, произведениями функций, а также с «функциями функций», то есть сложными функциями. Исходя из определения производной, можно вывести правила дифференцирования, облегчающие эту работу. Если C — постоянное число и f=f(x), g=g(x) — некоторые дифференцируемые функции, то справедливы следующие правила дифференцирования:
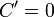
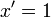

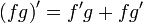
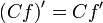
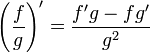
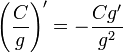
Если функция задана параметрических:

Дифференцирование сложной функции:
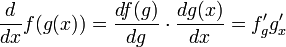
Формулы производной произведения и отношения обобщаются на случай n-кратного дифференцирования (формула Лейбница):
 где
где  — биномиальные коэффициенты.
— биномиальные коэффициенты.
Следующие свойства производной служат дополнением к правилам дифференцирования:
если функция дифференцируема на интервале  , то она непрерывна на интервале
, то она непрерывна на интервале  . Обратное, вообще говоря, неверно (например, функция
. Обратное, вообще говоря, неверно (например, функция  на
на  );
);
если функция имеет локальный максимум/минимум при значении аргумента, равном  , то
, то  (это так называемая лемма Ферма);
(это так называемая лемма Ферма);
производная данной функции единственна, но у разных функций могут быть одинаковые производные.

Таблица производных некоторых функций
Функция 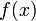
| Производная 
| Примечания |
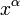
| 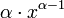
| Доказательство:
Фиксируем  , придадим приращение аргументу , придадим приращение аргументу 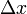 . Вычислим приращение функции: . Вычислим приращение функции: 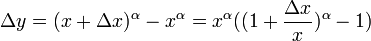 , т.о , т.о
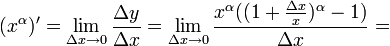

|

| 
| Доказательство:
Фиксируем  , придадим приращение аргументу , придадим приращение аргументу 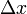 . Вычислим приращение функции: . Вычислим приращение функции:
 , т.о , т.о


|
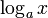
| 
| |

| 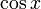
| |
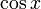
| 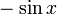
| |
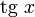
| 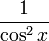
| |

| 
| |
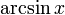
| 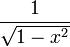
| |

| 
| |
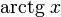
| 
| |

| 
| |
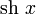
| 
| |

| 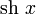
| |

| 
| |

| 
|
Глава 3 «Неопределённый интеграл»
Неопределённый интеграл для функции 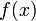 — это совокупность всех первообразных данной функции.
— это совокупность всех первообразных данной функции.
Если функция 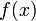 определена и непрерывна на промежутке
определена и непрерывна на промежутке  и
и  — её первообразная, то есть
— её первообразная, то есть 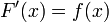 при
при  , то
, то 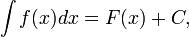
,
где С — произвольная постоянная.
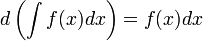
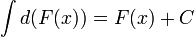

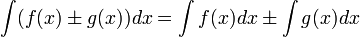
Если  , то и
, то и  , где
, где 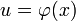 — произвольная функция, имеющая непрерывную производную.
— произвольная функция, имеющая непрерывную производную.
Подведение под знак дифференциала
При подведении под знак дифференциала используются следующие свойства:


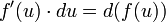
Основные методы интегрирования
1. Метод введения нового аргумента. Если
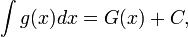
то

где  — непрерывно дифференцируемая функция.
— непрерывно дифференцируемая функция.
2. Метод разложения. Если
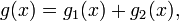
то

3 Метод подстановки. Если  — непрерывна, то, полагая
— непрерывна, то, полагая

где 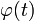 непрерывна вместе со своей производной
непрерывна вместе со своей производной  , получим
, получим

4 Метод интегрирования по частям. Если  и
и  — некоторые дифференцируемые функции от
— некоторые дифференцируемые функции от  , то
, то

Таблица основных неопределённых интегралов

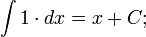
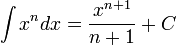
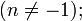

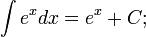



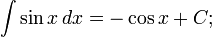

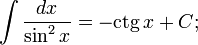

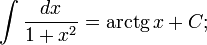
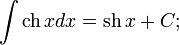

Слева в каждом равенстве стоит произвольная (но определённая) первообразная функция для соответствующей подынтегральной функции, справа же — одна определённая первообразная, к которой ещё прибавляется константа  такая, чтобы выполнялось равенство между этими функциями.
такая, чтобы выполнялось равенство между этими функциями.
Первообразные функции в этих формулах определены и непрерывны на тех интервалах, на которых определены и непрерывны соответствующие подынтегральные функции. Эта закономерность не случайна: как отмечено выше, всякая непрерывная на интервале функция имеет на нем непрерывную первообразную.
|
|
|
|
|
Дата добавления: 2014-12-17; Просмотров: 838; Нарушение авторских прав?; Мы поможем в написании вашей работы!