Примеры вычисления определённых интегралов

Примеры вычисления неопределённых интегралов

Вычисление интеграла по таблице

= dx =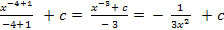

;

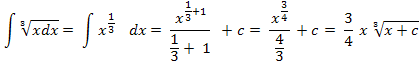
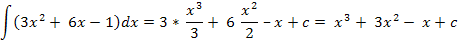
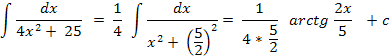
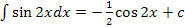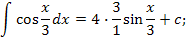
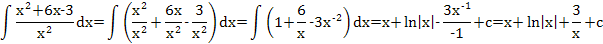
Интегрирование подстановкой:

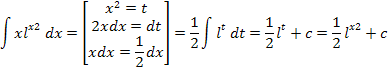
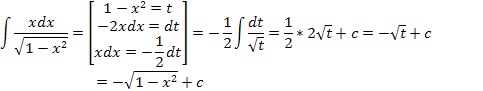
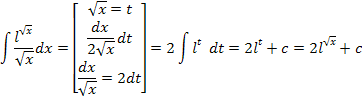
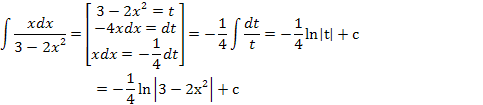
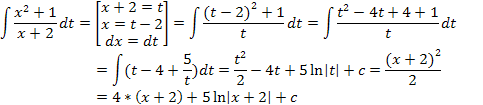
Примеры вычисления интегралов

Основная формула Ньютона – Лейбница

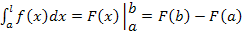
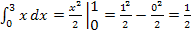
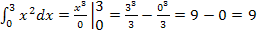
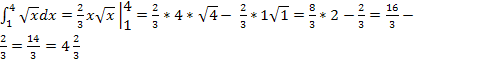
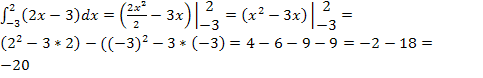
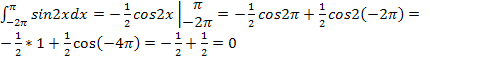
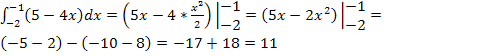
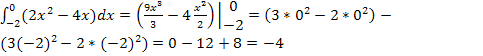
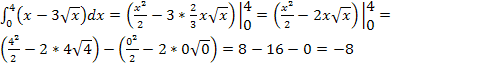
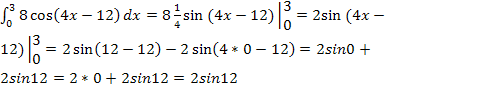
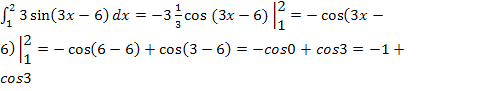
Вычисления подстановкой

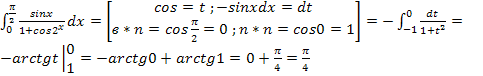
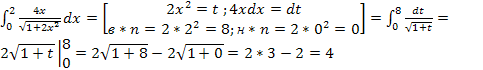
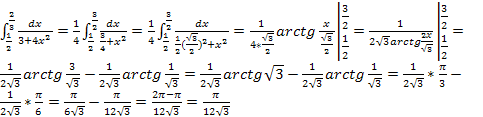
Глава 4 Дифференциальные уравнения.

Дифференциальным уравнением называется уравнение, связывающее между собой независимую переменную х, искомую функции у и ее производные или дифференциалы.

Символически дифференцированное уравнение записывается так:

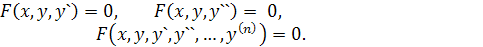
Дифференциальное уравнение называется обыкновенным, если искомая функция зависит от одного независимого переменного.

Порядком дифференциального уравнения называется порядок старшей производной (или дифференциала), входящей в данное уравнение.

Решением (или интегралом) дифференциального уравнения называется такая функция, которая обращает это уравнение в тождество.

Общим решением (или общим интегралом) дифференциального уравнения называется такое решение, в которое входит столько независимых произвольных постоянных, каков порядок уравнения. Так, общее решение дифференциального уравнения первого порядка содержит одну произвольную постоянную.

Частным решением дифференциального уравнения называется решение, полученное из общего при различных числовых значениях произвольных постоянных. Значения произвольных постоянных находятся при определенных начальных значениях аргумента и функции.

График частного решения дифференциального уравнения называется интегральной кривой.

Общему решению дифференциального уравнения соответствует совокупность (семейство) всех интегральных кривых.

Дифференциальным уравнением первого порядка называется уравнение, в которое входят производные (или дифференциалы) не выше первого порядка.

Дифференциальным уравнением с разделяющимися переменными называется уравнение вида

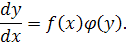
Для решения этого уравнения нужно сначала разделить переменные:

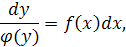
а затем проинтегрировать обе части полученного равенства:

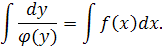
1. Найти общее решение уравнения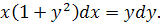

o Разделив переменные имеем

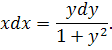
Интегрируя обе части полученного уравнения:

Так как произвольная постоянная С может принимать любые числовые значения, то для удобства дальнейших преобразований вместо C мы написали (1/2) ln C. Потенцируя последнее равенство получим

Это и есть общее решение данного уравнения.

Литература

В. Г. Болтянский, Что такое дифференцирование, «Популярные лекции по математике»,

Выпуск 17, Гостехиздат 1955 г., 64 стр.

В. А. Гусев, А. Г. Мордкович «Математика»

Г. М. Фихтенгольц «Курс дифференциального и интегрального исчисления», том 1

В. М. Бородихин, Высшая математика, учеб. пособие, ISBN 5-7782-0422-1.

Никольский С. М. Глава 9. Определенный интеграл Римана // Курс математического анализа. — 1990. — Т. 1.

Ильин В. А., Позняк, Э. Г. Глава 6. Неопределенный интеграл // Основы математического анализа. — 1998. — Т. 1. — (Курс высшей математики и математической физики).

Демидович Б.П. Отдел 3. Неопределенный интеграл // Сборник задач и упражнений по математическому анализу. — 1990. — (Курс высшей математики и математической физики).

Валуцэ И.И., Дилигул Г.Д. Математика для техникумов на базе средней школы: Учеб.пособие-2-е изд.перераб. и доп. М.6Наука. 1989

Колягин Ю.М. Яковлев Г.Н. математика для техникумов. Алгебра и начала анализа 1 и 2 часть. Издательство «Наукка» М., 1981г.

Щипачев В.С. Задачи по высшей математике: Учеб. Пособие для вузов. Высш. Шк. 1997г.

Богомолов Н.В практические занятия по математике: учеб. Пособие для техникумов. Высш. Шк 1997г.

Дата добавления: 2014-12-17