График 1. 3 страница

И потому для нас течение собственного времени всех тел коррелируется с коэффициентом k. А это позволяет в первом приближении считать время абсолютным, единым, однонаправленным процессом последователь­ного совершения различных событий для каждого тела, т.е. приписывать природе, как это сделал И. Ньютон, единое математическое время.

Собственно для Земли временем является период вращения ее гравиполя (период пульсации). Период может определяться несколькими способами из пара­метров орбитального движения пробного тела у поверх­ности, линейной скорости v, угловой частоты w и длины волны Земли λ. Эти параметры связаны уравнением:

v = λw,

но Т - величина, обратная периоду пульсации w:

w = 1/Т,

Отсюда период пульсации Земли τ равняется:
τ = λ/v = 5024 с.. (1.16)

Период пульсации τ и есть собственное локальное время Земли. Из формулы (1.16) и из инварианта:

R³/τ² = const.

следует, что период собственной пульсации не остается неизменным для пространства с удалением от поверх­ности Земли (это следствие анизотропности про­странства).

Жизнь на планете Земля определяется частотой пуль­сации планеты. Любое другое небесное тело, как и от­крытый космос, имеют свою частоту пульсации, отлич­ную от пульсации Земли. Биосфера Земли в целом или ее составляющие отдельно в своем естественном виде не могут прижиться на других небесных телах.

Именно дисбаланс колебаний внешнего пространства и тел космонавтов обусловливают их состояние при длительных орбитальных полетах. Поэтому для сохра­нения нормального здоровья при передвижении в кос­мосе они должны поддерживать и у себя, и на аппара­тах, на которых двигаются, ритм пульсации планеты Земля, т.е. время Земли.

Поскольку время есть период собственного колебания каждого тела, определяемый как свойствами самого те­ла, так и взаимодействием его с внешними телами и пространством, то движение тела в пространстве с любой скоростью и в любом направлении сопровожда­ется изменением периода его собственной пульсации, вызываемого взаимодействием с этим пространством. Именно это взаимодействие создает реальный, а не ка­жущийся эффект замедления течения локального вре­мени движущегося тела. Это замедление существует реально при движении с любой скоростью и может быть проверено эмпирически.

Таким образом, физическое время есть свойство соб­ственной пульсации каждого тела. Оно связано со все­ми его свойствами в единую систему, описываемую ко­эффициентами физической размерности (КФР, рассма­тривается далее) и отображаемую через период годового движения Земли.

Несколько слов о влиянии процесса насыщения и пульсации на существование живых существ.

Все тела, включая живые существа, насыщаются эфи­ром в различной степени. Живые существа насыщаются на амерном уровне и, по-видимому, в процессе передачи наследственности закрепляют достигнутый период пульсации и получают в зародышевом состоянии возможность самопульсации, имеющей период, больший, чем период пульсации Земли в этот момент. В процессе роста и разви­тия период их пульсации возрастает медленнее, чем пе­риод пульсации Земли, и где-то к середине жизни орга­низма период его пульсации сравнивается с периодом пульсации Земли, а затем начинает отставать. Так начи­нается старение.

Естественно, что все составляющие живое существо органы пульсируют в унисон с другими органами и с телом в целом. Изменение собственной пульсации лю­бого органа вызывает его заболевание и приводит либо к его отторжению, либо к заболеванию всего тела. По­следнее характеризуется нарушениями не только ритма пульсаций, но эфирного обмена, что может иметь пе­чальный исход. Каждое живое тело имеет собствен­ный, строго индивидуальный период пульсации, кото­рый и определяет время его жизни.

1.7. Плотностная мерность пространства

Вероятно, первым, кто связал мерность пространства с взаимодействием, был один из величайших немецких философов Эммануил Кант. В своей студенческой рабо­те с длинным названием «Мысли об истинной оценке живых сил и разбор доказательств, которыми пользова­лись г-н Лейбниц и другие знатоки механики в этом спорном вопросе, а также некоторые предварительные соображения, касающиеся сил вообще», он изложил свои соображения об истинной мере движения на 180 страницах, и только на трех из них касается трехмерно­го пространства [27]. Но именно на этих страницах по­является мысль, отражающая суть трехмерности про­странства: «Трехмерность происходит, по-видимому, оттого, что субстанции в существующем мире дей­ствуют друг на друга таким образом, что сила дей­ствия обратно пропорциональна квадрату расстоя­ния».

Это высказывание И. Канта пытаются, сам он об этом не упоминал, связать с представлением об относительной природе пространства (лейбницево пространство — отношение тел в отличие от концепции ньютоновского абсолютного пространства, не зависящего от тел и явле­ний), но можно понимать его и по-другому и тоже в аб­солютной форме. Пространство — вещественное абсо­лютное образование-субстанция (как абсолютны все без исключения тела), включающая другие тела-пространства (почему-то часто забывается, что каждое тело само образует свое пространство), взаимодейст­вующая с ними и передающая взаимодействие пропор­ционально квадрату расстояния между ними.

Такое понимание высказывания И. Канта придает пространству все свойства тел, делает его подобным те­лам и потому взаимодействующим с ними. В то же время оно своими размерами превосходит все включае­мые тела, создавая вместе с ними телесное вместилище, некий симбиоз, обладающий но­вым качеством — «пространство».

Следует отметить, что понятие «расстояние», которое входит основным элементом в представление о про­странстве, к которому мы буквально «прикипели», в природе как некий размер отсутствует. Рас­стояние, как определенная количественная величина длины, соизмеренная с эталонным отрезком, независи­мым от природных процессов, ощущается только на­блюдателем. Природа ими не излишествует. То, что мы измеряем метрами, в природе обусловлено движением и некоторым взаимодействием, связанным с пульсацией измеряемого тела. И эта пульсация, характер которой еще достаточно непонятен, имеет некоторый центр R, относительно которого что-то, похоже, гравитационное поле, имеет линейную скорость v и угловую частоту ω. Т.е. тело и его поле пульсирует, колеблется или вращается, но не оста­ется неподвижным. Уравнение же, связывающие эти па­раметры, в механике хорошо известно:

R = v/ω,

или с использованием периода τ:

R = vτ.

Из этих уравнений следует, что расстояние в природе, обозначаемое длиной отрезка R, не есть неподвижная элементарная длительность или дистанция, а характе­ризуется количественной величиной некоторого волно­вого движения — произведением скорости на период.

Однако понимание того, что расстояние не есть отре­зок чего-то и не определяется жестким эталоном длины, а является произведение подвижных волновых парамет­ров и потому имеет, прямо или косвенно, динамический характер, еще не устоялось в науке. Следовательно, и отношение к характеристике мерности не учитывает эти особенности природы расстояний. А поскольку само­пульсация тел и пространства является определяющим фактором их самодостаточности, если всякое расстоя­ние есть следствие взаимосвязанного процесса скорости и частоты объемной пульсации тел в любой области пространства, то ответ на вопрос о том, какую мерность имеет наблюдаемое пространство, достаточно очевиден — пространство трехмерно. Оно трехмерно потому, что при количестве принятой пространственной мерности >3<, как доказано математически, волновые процессы происходить не могут, орбиты планетные и электрон­ные оказываются незамкнутыми, структура светового спектра будет отличаться от наблюдаемого.

Математически можно оперировать бесчисленным множеством пространств, если исходить из того, что расстояние есть самонеподвижная данность, получаемая посредством измерения промежутков между самоне­подвижными телами или их частями неким стандарт­ным измерительным инструментом. И, пользуясь таким инструментом и постулатом о самонеподвижности тел, можно получить множество механик с великолепным математическим аппаратом, начиная с механики И. Ньютона, способных рассчитывать множество факто­ров, и не имеющих никакого отношения к природным явлениям.

Однако для понимания структуры пространства того факта, что оно имеет три измерения, недостаточно. Трехмерность пространства подтверждает и то, что в каждой его области имеется множество выделенных пульсирующих то­чек — центров ячеек, структурирующих вещественное пространство вокруг себя, и от­гораживая его от соседнего пространства, непреодолимой для них нейтральной зо­ной. И то, что к центру каждой ячейки вещественная плотность пространства возрастает. И то обстоятельст­во, что с возрастанием этой плотности количественные величины всех параметров пространства и тел, находя­щихся в нем, изменяются. И изменяются таким образом, что мыслящие существа, например, на планетах некото­рой звездной системы считают эти параметры одинаковыми для всех планет (в частно­сти аналогичного мнения придерживаются земляне).

Следует отметить, что наличие множества точек-центров пространства и неоднородная плотность веще­ства в объеме обусловливают прохождение по нему множества различных колебаний и как следствие изме­нение по объему всех физических размеров и в том числе постоянной π. И это изменение плотности, вызывающее изменение постоянной π, можно принять за количественное отображение плотностной пространст­венной мерности. То есть принятая в физике трехмер­ность отображает не многомерность пространства n, а его равновеликую (приблизительно) мерность по координатным осям. Естественно, что изменение плот­ности пространства и тел (деформация) происходит в различных областях с неодинаковой скоростью и на различные величины. Но оно не меняет физической сущности пространства и во всех направлениях от центра имеет характер приращения ±∆. И, потому от­носительно координат становятся безразмерными ко­эффициентами различной по объему гравитационной деформации. Именно по этой причине оси трёх направ­лений пространства имеют одинаковую мерность в пространстве объема, но по направлениям каждой из осей х, у, z, начиная от нулевой точки, ¾ не на равную ве­личину. Однако это неравенство на эквипотенциальной поверхности сопровождается настолько незначитель­ным изменением мерного инструмента, что в практике нами не регистрируется, но наличествует и имеет, на­пример, существенное значение для оси z.

Другое дело в мировом космическом пространстве или пространстве микромира. Поскольку структура этих пространств одинакова и отличается только количественной величиной динамической плотности пространственных областей, и в космосе и в молекулах переход изодной плотности пространства (одной мер­ности) в другую плотность (другую мерность) должен сопровождаться качественным скачком с явной или не­явной границей, отграничивающей одно пространство от другого. Наличие такой границы фиксируется и в космосе (например, центральная прозрачная область Га­лактики, как известно, плотное вещество), и на поверх­ности Земли (переход от качественно отличающегося по плотности космического пространства к пространству глубин Земли имеет своей границей поверхность по­следней), и в микромире. Так, постоянная тонкой струк­туры α = 137, вероятно, сигнализирует о такой границе вструктуре атома, так же как и величина 1836, которую мы принимаем за отношение массы протона к мас­се электрона.

2. Введение в основы

русской геометрии

2.1. Динамика аксиомы о параллельных

Прежде чем очень кратко познакомиться с основами русской (динамической) геометрии вспомним весьма важное для ее понимания понятие «бесконечность». Она качественно мыслится в пространстве как бесконечность наружу или «вширь» (в смысле отсутст­вия внешних границ) и как бесконечность вглубь (в смысле бесконечной делимости). В свою очередь каче­ственная бесконечность имеет две градации: одна — как движение, нескончаемый процесс, постоянное станов­ление (потенциальная бесконечность), другая — как не­что данное, имеющееся, наличное бытие (актуальная не кантовская бесконечность).

Именно использование понятия "бесконечность" в ос­нованиях геометрии определяет ее структуру [28]. Так, опора на актуальную бесконечность предполагает суще­ствование трехмерного не качественного метрического пространства, заполненного неподвижной (статической) изотропной материей, структурированной по иерархии равнозначных бесконечностей, при полном отсутствии движения и, следовательно, времени. Все геометрии, и в первую очередь геометрия Евклида, построены с ис­пользованием свойств актуальной бесконечности и по­тому являются геометриями статическими.

Потенциальная бесконечность предполагает матери­альность (телесность) безграничного пространства и его всеобщее бесконечное самодвижение (динамику). По­этому первичные понятия геометрии, построенной на свойствах потенциальной анизотропной бесконечности, отличаются от первичных понятий актуальной геомет­рии не только движением, но и структурой. Геометрии, отражающей потенциальную бесконечность, еще не по­строено, но можно отметить, что она будет качественно отличаться от статических геометрий, нагляднее ото­бражать явления природы, а, следовательно, и точнее описывать их. К тому же «замораживание» движения элементов динамической геометрии в определенном по­рядке обусловливает возможность построения любой статической геометрии, и, следовательно, все они ока­зываются произ-водными от нее. А теперь обратимся к аксиоме о параллельных Евклида.

В Евклидовой геометрии, созданной в III в. до н.э., на основе незначительного количества априорных аксиом выводятся все ее теоремы. Однако пятая аксиома ¾ ак­сиома о параллельных — по содержанию больше напо­минает теорему. Но многочисленные попытки предста­вить ее в виде теоремы оказались неудачными. До нашего времени она дошла в следующей формулировке:

«Через точку, лежащую на плоскости вне прямой, можно провести одну и только одну прямую, параллельную данной».

В этой формулировке постулируется несколько поло­жений, нарушающих условия статичности:

• геометрия Евклида статична, а в формулировку за­ложено движение (динамика), к тому же в неявной фор­ме ¾ на бесконечности;

• условия движения на бесконечности не определены, а потому возможно движение без взаимодействия с про­странством или во взаимодействии с ним. В последнем случае взаимодействие будет проявляться в искривле­нии линии;

• постулируется, и тоже неявно, возможность дли­тельного движения прямой, которое возможно только во времени. Статическая же геометрия времени не содер­жит.

Таким образом, аксиома о параллельных сформулиро­вана неопределенно и потому может иметь несколько дефиниций. И действительно в XIX в. сначала Лобачев­ский, а затем Риман предложили еще две формулировки аксиомы о параллельных. Лобачевский предположил, что:

«Через точку на плоскости, лежащую вне прямой, можно провести бесконечное множество прямых, параллельных первой».

И построил на этой основе логически непротиворечи­вую геометрию отрицательной кривизны. Геометрия положительной кривизны сформулирована Риманом как отрицание постулата Лобачевского:

«Через точку на плоскости, лежащую вне прямой, невозможно провести ни одной прямой, параллельной первой».

И на этой основе была построена логически непроти­воречивая сферическая (? – А.Ф.) геометрия.

Итак, мы имеем три двойственных формулировки ак­сиомы о параллельных: Евклида, Лобачевского и Римана. Все они базируются на использовании как свойств актуальной, так и потенциальной бесконечности [28]. Возникает вопрос: можно ли сформулировать аксиому о параллельных на основе только свойств потенциальной бесконечности?

Отметим еще раз, что основное свойство потенциаль­ной бесконечности ¾ движение, которое остается не­завершенным на бесконечности. Воспользовавшись этим свойством, сформулируем аксиому о параллель­ных:

Следы-прямые, образованные движущимися к еди­ному центру из разных областей пространства точ­ками и не достигающими этого центра за бесконечный промежуток времени, ¾ параллельны.

В этой аксиоме предполагается, что следы ¾ прямые, образуе­мые движущимися точками, совместно стремятся к еди­ному центру, который может находиться в любой точке пространства, но оставаться недостижимым, поскольку свойства напряженности пространства изменяются и своим изменением замедляют их движение (вспомните температурную сферу А. Пуанкаре). Каждый после­дующий шаг для них оказывается меньше предыдущего, и поэтому расстояние до центра О не может быть прой­дено даже за бесконечный промежуток времени. То есть эти движущиеся прямые никогда не пересекутся и, сле­довательно, они параллельны. Геометрия, основанная на данной аксиоме, является динамической или физической геометрией.

Следует отметить, что для этой геометрии становится неприменимым евклидово понятие "прямая линия", поскольку последняя не проходит через две существую­щие точки. Вероятно, более подходит следующее опре­деление: Прямая линия — след точки движущейся к дру­гой точке по кратчайшему пути. Евклидово определение понятия "точка" можно временно сохра­нить.

Рассмотрим, к каким последствиям приводит эта ак­сиома (рис. 8).

Предположим, что из точки А к точке О движется тело-точка и за прошедшее время она прошла расстояние АА, след- траектория которо­го есть прямая ли­ния. Будем назы­вать ее прямой. Одновременно из точки А' к тому же центру О движется другое тело-точка. И эта точка прошла расстояние А'А'. Ее след-траектория тоже прямая линия или просто прямая,

Рис. 8

как и след всех последующих точек. Прямые АА и А'А', ос­тавленные движущимися точками, по геометрии Евкли­да не являются параллельными.

Но в динамической гео­метрии они параллельны, поскольку никогда не в состоянии достичь центра О и, следовательно, пере­сечься в одной точке. К тому же, в отличие от «прямых» Лобачевского и Римана, они действительно прямые. Определим, какие зависимости возникают между дви­жением этих прямых и элементами фигур, образуемых ими. Продолжим построение (рис. 9). Проведем допол­нительные прямые АА', А"А",... АⁿАⁿ так, чтобы по длине они оставались равными между собой, а расстоя­ние между ними определялось отрезком, выходящим из некоторой точки k прямой АА до точки k', лежащей на прямой А'А' под углом Akk' к прямой А′А' и равным ему углом А'kk' прямой АА.

След следующей прямой проводим по тем же правилам из точки k ' прямой А'А' к точке k" прямой А"А". И так до тех пор, пока отрезок, выходящий из точки kⁿ прямой А^пАⁿ, не замкнет построение ломаной на прямой АА. Поскольку расстояние между прямыми одина­ково, а углы на пересе­чении каждого отрезка с прямой равны, замы­кающий отрезок попа­дет в ту же точку k прямой АА, из которой вышел отрезок kkⁿ. Замкнутая ломаная kk'k"...кⁿ образует равносто­ронний многоугольник. В результате получаем на плоскости «частокол» пря­мых, имеющих своим стремлением недостижимый в бесконечности, а потому фиктивный, центр О. Все пря­мые в своем движении к недостижимому центру парал­лельны и по определению и по структуре напряженно­сти на поверхности плоскости. А основная особенность образовавшегося правильного многоугольника ¾ дихо­томия конечного и бесконечного в том, что конечный периметр замыкает в себя площадь бесконечной вели­чины. Если теперь через центры отрезков, образующих стороны многоугольника kk′ k'k", k"k"',…, kⁿk, провести новые прямые и соединить их отрезками по правилам, изложенным выше, то получим многоугольник с коли­чеством сторон, превышающем количество первого в два раза. При продолжении этой операции бесчисленное число раз длина отрезков kk', k'k",..., k"k будет стремиться к минимуму, а углы Аkk', А'k'k′′ А′'k′'k′",... устремятся к π/ 2, и в пределе многоугольник kk′k′′ …kⁿ долженпревратится в окружность на плоскости. Плоскость окружности одно­временно будет обладать свойствами евклидовой стати­ческой геометрии, и содержать в своих границах пло­щадь конечной величины, и свойствами неевклидовой геометрии и содержать в тех же границах площадь ве­личины бесконечной. Две несовместимые площади как бы налагаются друг на друга.

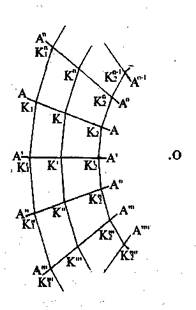
Рис. 9.

В полном соответствии с геометрией Евклида длина окружности S будет равна 2 π радиан, а радиус, напро­тив, будет стремиться к бесконечности, никогда не дос­тигая центра О. Последний в данном случае, отсутству­ет. Прямая может исходить из какой-то точки окружности или входить в нее, но никогда не может пройти бесконечность. В то же время, по геометрии Евклида, центр у данной окружности S имеется, длина ра­диуса R конечна и определяется уравнением R = S/ 2 π.

Получается, что одни и те же геометрические элемен­ты можно одновременно мерить и жесткими стержнями (геометрия Евклида) и динамическими. А это означает, что между геометрией статической и динамической имеется определен­ная взаимосвязь. Попробуем ее отыскать.

Отложим от точки k вправо и влево (см. рис.9) по от­резку kk₁ и kk₂ одинаковой длины в евклидовой мерно­сти и, используя предыдущее правило построения, про­ведем через них еще две окружности k₁'k₁"k₁′"... k₁ⁿ и k₂′k₂′′k₂′′′… k₂ⁿ. Естественно, что окружности k₁ и k₂ по от­ношению к окружности k будут описанной и вписанной. И это единственное, что общее, как для евклидовой, так и для неевклидовой геометрии.

Отличие же их начинается уже с того, что наружу от окружности обе геометрии допускают проведение бес­счетного числа окружностей на одинаковом расстоянии друг от друга, а внутри окружности k, по геометрии Евклида, число таких окружностей ограничено, для динамичёской же геометрии — снова не ограничено. Каж­дая окружность — эквипотенциальная линия относительно точки О. И длина ее (или окружность) равна бес­конечности одного ранга, т.е. они равны между собой. Это есть следствие аксиомы о динамических параллель­ных. Оно может быть сформулировано следующим об­разом:

Дуги-хорды kk', k₁k₁′, пересекающие прямые АА и А'А' под одним углом и на некотором расстоянии друг от друга, имеют одинаковую длину.

Это следствие — теорема требующее доказательства. В настоящей работе она предлагается как аксиома. И на ее основе получается, что:

• В геометрии Евклида длина всех окружностей раз­лична, а в неевклидовой одинакова. Линия же окружно­сти является прямой.

• В геометрии Евклида линия окружности непрерыв­на, а в неевклидовой дискретна и состоит из бесчислен­ного множества одинаковых отрезков бесконечной дли­ны.

• В статической геометрии радиус окружности коне­чен, в динамической бесконечен.

• В статической геометрии взаимодействие между ра­диусом и окружностью отсутствует, в динамической на­личествует.

• Статическая геометрия радиусы и окружности не связывает со временем, в динамической такая связь имеется и т.д.

Таким образом, отсутствие одинаковых качеств у ок­ружностей двух геометрий лишает нас возможности оп­ределения взаимосвязи между ними по качественным признакам и вынуждает использовать свойства несоиз­меримых чисел (что вполне понятно, поскольку конеч­ное и бесконечное несоизмеримы по определению). Возьмем, например, два евклидовых круга одинакового радиуса r и площадью S. Сложим площади вместе так, чтобы образовался новый круг в два раза большей пло­щадью S' и определим, насколько радиус R нового круга больше радиуса r маленького круга. Площадь большого круга S'= πR², малого S = πr²:

πR² = 2 r²π R = r√2= 1,41421... r.

Число √2, по Дедекинду, и есть несоизмеримое ирра­циональное число, символ особого способа распределе­ния соизмеримых чисел [9]. В динамической геометрии, однако, это символ связности, а в данном случае — каче­ственный коэффициент, обусловливающий изменение пространства при движении в нем двух линий к отда­ленному центру. При коэффициенте связности, равном √2, две линии, движущиеся на плоскости к одному цен­тру, всегда параллельны, или, что то же самое, никогда не пересекаются на бесконечности. При устремлений √ 2→ 1 соизмеримость бесконечности меняется, и при достижении 1 динамическая геометрия переходит в статическую геометрию Евклида на плоскости.

Определим, чему равно несоизмеримое число, описы­вающее пространство. Используем метод построения окружности при образовании сферы. Для этого прове­дем множество одинаковых прямых АА, параллельных А′А′, направленных к единому центру, но не в плос­кости, а в объеме, и получим «ежик» прямых, устремленных в одну точку, на бесконечности. Пересечем их прямыми, исходящими из точки k₁, по ранее описанному методу. В результате по­строения получаем сферический многогранник, Сходя­щийся при бесчисленном увеличении граней в правиль­ную сферу, имеющую конечную площадь поверхности, но бесконечную длину радиуса.

Имеется и более простой способ построения сферы путем вращения образовавшегося круга вокруг прямой, например, АА (Рис. 9.), становящейся осью вращения, а при повороте на минимальные градусы «втыкаются» прямые, направленные к центру. Но при этом создается иллюзия, что образовавшаяся сфера име­ет выделенную ось вращения, и ось эта — прямая, про­ходящая через центр сферы. В данной же сфере ни одна прямая, входящая в сферу и идущая к центру, до него не доходит и тем более его не проходит.

Любым из этих способов можно построить бесчис­ленное количество сфер как внутренних, так и внешних по отношению к базисной сфере k, объем каждой из ко­торых будет конечен в евклидовой геометрии и беско­нечен в динамической. И если объем всех евклидовых сфер геометрически различен, то объем неевклидовых сфер физически равен друг другу, т.е. обладает тем же соотношением качеств, что и окружности.

Теперь, исходя из метричности евклидовых объемов сфер, определим величину коэффициента объемной связности (объемное число Дедекинда). Мысленно вы­членим внутри одной сферы V другую таким образом, чтобы объем вычлененной сферы V_о и объем сферы V₁ между поверхностями двух сфер были равны: V = V_о, тогда суммарный объем V равен:

V = 4/3 πR³ = V₁ + V = 2 V = 8 / 3 πR³.

Определим, насколько радиус внешней сферы R превы­шает радиус внутренней r, R³ = 2 r³.

Отсюда: R = ³√2 r = 1,259921... r. k = 1,259921.

Таким образом, коэффициент связности объема k (не­соизмеримое число Дедекинда) равно: k = ³√2 = 1 259921.... Это число, как и коэффициент связности окружности, является иррациональным и обусловливает бесконечное движение параллельных к центру сферы.

Хотя коэффициент связности и является безразмерностной величиной, он качественно индивидуален для каждого параметра. Говоря словами Дедекинда, каждый коэф­фициент принадлежит своему и только своему рангу па­раметров, а потому для каждого из них необходима соб­ственная индексация.

2.2. Структурирование динамического

пространства

Известно, что проблема бесконечного включает дихо­томию взаимосвязи двух пар категорий, с одной сторо­ны, различие конечного и бесконечного, с другой — по­коя и движения. Попарное существование противо­положных форм категорий обусловливает различие в подходе к описательному отобра-жению космических тел и структур. Это различие прежде всего относится к первичным понятиям: тело-точка, прямая-луч, плос­кость, движение и т.д.

Выше было показано, что тело в динамической гео­метрии представляет материальную сферу, бесконечную внутрь и отграниченную собственной поверхностью от окружающего пространства. Тело, как вещественное об­разование, формирует структуру и влияет на внешнее пространство в соответствии с энергетической на­пряженностью, создаваемой количественной величиной всех своих свойств.

Дата добавления: 2014-11-29