График 1. 5 страница

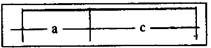
Золотое число Ф = 1,618... получается несколькими способами, оно из которых — деление отрезка в край­нем и среднем отношении. Отметим, что в постановке задачи говорится о делении одного отрезка на две не­равные части а и с так (рис. 16), чтобы весь отрезок (а + с) относился к большей части с, как с к меньшей части а. Запишем это отношение:

(а + с)/с = с/а (2.1)

Рис. 16

Пропорция (2.1) носит название золотой. В данном случае подразумевается конечная в рациональных чис­лах длина отрезка (а + с), кратная некоторому изме­рительному инструмен­ту. В условии задачи нигде не говорится о невозможности его целочисленного или дроб­ного рационального деления и о нерациональности двух (?) образующихся при делении отрезков.

Это очень важная оговорка. Она подтверждает непреднамеренный, а как бы вероятностный или даже случайный характер деления. Проверим эту случай­ность. Проведем решение (2.1), заменив отношение с∕а нa b:

b = c / a, (2.2)

и, подставив (2.2) в (2.1), получаем квадратное уравне­ние

b² – b – 1 = 0, (2.3)

решая которое, находим величину b:

b₁ = (1 + √5) / 2= Ф = 1,6180339, (2.4)

b₂ = (l – √5)/2 = – 1/ Ф = – 0,6180339. (2.4)

Золотое число Ф – является числом иррациональным. То есть таким числом, бесконечная последо­вательность которого не может быть вычислена до конца, сколько бы времени его ни вычисляли.

Отмечу, что любое иррациональное число — не коли­чественное число. Оно индивидуально, не имеет одно­значного количественного выражения и отображает своего рода математическое качество. Оно отражает неограниченную количественную величину и не может точно складываться как с рациональными, так и с ирра­циональными числами (качества не складываются). Оно квантованный (выделенный из числового ряда) элемент числового ряда, обособленный от него и не примыкаю­щий ни к одному большему или меньшему числу. Все операции с ним проводятся с приблизительной точно­стью. Повторяю — это качественная индивидуальность, и, следовательно, бесконечный ряд иррациональных чи­сел не является дурной бесконечностью. С нахождени­ем иррационального числа в математику входит пред­ставление о математическом качестве и квантовании чисел, вне зависимости от того, осознали это математи­ки или нет. Квантованное иррациональное число — осно­ва и предтеча квантованной геометрии. Но вернемся к Ф.

Получив Ф и ее обратную величину, т.е. два числа, мы успокаиваемся, так и не определив, а чему же равны числа а и с в формуле (2.1) и какое отношение они име­ют к b, тем более, что подстановка b в (2.2) с после­дующим выходом на (2.1) не приводит к определению величин а и с, а следовательно, и не решает поставлен­ную задачу.

Тогда зачем же мы находим b?Ответ — только для того, чтобы получить точную величину Ф, поскольку знаем, что это число — основа золотой пропорции. Но что скрывает это число? В чем суть золотой пропорции?

Попробуем решить (2.1) другим путем. Умножим чис­литель и знаменатель левой части отношения (2.1) на а, правой на с и, сократив знаменатели, получаем следую­щее уравнение:

а² + ас = с². (2.5)

Уравнение (2.5) по количественной величине а и с оказывается полностью неопределенным. Ее члены, хо­тя и зависимы друг от друга, могут составлять пропор­ции при любых числовых значениях одного из них. Ес­ли же в (2.5) вместо ас подставить

b² = ас, (2.6)

то уравнение (2.5) из простой пропорции превратится в теорему Пифагора:

а² + b² = с². (2.7)

Поскольку операция замены ас на b² при данных ог­раничениях возможна только в единственном случае, когда а = √Ф, то в исполнении (2.7) числа а, b, с оказы­ваются однозначно связанными с золотым числом Ф. И, как следствие, члены уравнения (2.7) становятся гео­метрически квантованными относительно золотого числа. Какую бы количественную величину они не име­ли они всегда остаются степенью числа Ф. Появление квантованной по золотому числу Ф геометрической за­висимости свидетельствует о возможности построе­ния геометрии на квантованных числах или, иначе гово­ря, о возможности построения квантованной гео­метрии. Но вернемся к уравнению (2.7), которое описывает равенство суммы квадратов катетов прямо­угольного треугольника квадрату гипотенузы. В нем индекс b численно отображает большой катет прямо­угольного треугольника. И, следовательно, деление в крайнем и среднем отношении есть деление не на два отрезка, а на три, в пропорциях прямоугольного треугольника, в котором число b = Ф неявно занимает ме­сто одного из катетов. И вместо двух отрезков мы как бы получаем три, образующих новое геометрическое качество — прямоугольный треугольник. Наличие отно­шений (2.2) и (2.6) свидетельствует о существовании еще одного числа i, кратного а, b, с. Для получения i возведем в квадрат (2.2) и, подставляя в него значение b² из (2.6), имеем:

а² ·ас = с², (2.8)

с = а³.

Подставляя величину с из (2.8) в (2.2), получаем:

b = а².

И окончательно:

a⁶ = b³ = c².

Поскольку b имеет два значения b₁ = 1,618, и b₂ = 0,618, то по ним находим i₁, i₂:

i₁ = b³₁ = (1,618)³ = 4,2358,

i₂ = b³₂ = (0,618)³ = 0,236.

Извлекая из i₁ и i₂ корень шестой степени, получаем количественную величину а₁,а₂:

а₁ = ⁶ √ i₁ = ⁶√4,236 = 1,272,

а₂ = ⁶√ i₂ = ⁶√0,236 = 0,786.

Проведя извлечение квадратного корня из чисел i, на­ходим значения с:

с₁ = √i₁ = 2,058,

с₂ = √i₂ = 0,4858.

Выясним, какой модуль по длине, рациональный или иррациональный, имеет отрезок, делимый в крайнем и среднем отношении:

с₁ + а₁ = 3,33019... = а₁⁵.

Таким образом, в среднем и крайнем отношении де­лятся только иррациональные отрезки. А это может обо­значать одно — все естественные отрезки сами по себе и сами для себя имеют свою иррациональную метрику, несоизмеримую со стандартной (декретной) метрикой.

Следует обратить особое внимание на то, что способ деления отрезков в крайнем и среднем отношении с использованием теоремы Пифагора, по-видимому, един­ственный, обусловливающий нахождение восьми взаи­мосвязанных и пропорциональных Ф золотых чисел, образующих новый ряд, отличающийся от египетского пропорциональностью каждого числа «коэффициенту» 1,272...:

... 0,183; 0,236; 0,300; 0,382; 0,486; 0,618; 0,786; 1,000; 1,272; 1,618; 2,058; 2,618; 3,330; 4,236; 5,388;...

Этот удивительный бесконечный ряд иррациональных чисел, названный русским рядом, образующий набор подобных прямоугольных треугольников при придании любой последовательности троек чисел (например, 2,058; 2,618; 3,330; или 0,185; 0,236; 0,300) значимости отрезков. Треугольники образуются и при последова­тельном сдвиге чисел на одну или две цифры (напри­мер, 2,058; 2,618; 3,330 - один треугольник; 2,618; 3,330; 4,236 - другой; 3,330; 4,236; 5,388 - третий и т.д.) Создается впечатление, что они как бы нанизываются друг на друга, образуя невидимую цепочку.

Существование в золотом ряду чисел-отрезков, спо­собных образовывать прямоугольные треугольники, не может быть случайностью. Похоже, что они выпол­няют какую-то неизвестную нам функцию, определяе­мую степенями и последовательностью чисел ряда.

Но можно представить и другую картину. Имеется два ортогональных бесконечных катета, пересекаемых на пропорциональном иррациональном расстоянии парал­лельными линиями, отрезки которых превращаются в гипотенузы. А это уже не цепочка, а плоскость. И сразу же возникает предположение, что прямоугольные тре­угольники есть элементы прямоугольников, а их катеты — стороны прямоугольников. Продолжение катетов — оси координат х и у на плоскости, а гипотенузы — диаго­нали образовавшихся прямоугольников. И прорисовы­вающаяся естественным образом координатная сетка начинает походить на истоки некоей новой геометрии. Посмотрим, что еще скрывается в этом ряду.

Вернемся к теореме Пифагора об образующей плоско­сти и построим ее объемный аналог в трехмерном евк­лидовом пространстве. Проиндексируем любую последовательность из четырех чисел русского ряда исходя из того, что каждые три числа последовательности обра­зуют прямоугольник с двумя сторонами и диагональю: х, у, l, п, где l и n диагонали прямоугольников х, у, l и е, l, п. Они образуют следующие пропорции:

x² + y² = l²,

y_о² + l² = п².

Здесь у по количественной величине равно у_о, но ортоганально ему и х, а потому не складывается с у. Но бу­дучи ортогональной плоскости ху, у_о приобретает каче­ство третьей координаты – z, и потому, приравняв z = у_о, получаем плоскостной аналог теоремы Пифагора для «трехмерного» пространства:

х² + y² + z² = п². (2.9)

Перед нами достаточно странное уравнение (2.9). Числа одного математического ряда своей взаимосвязью демонстрируют изменяемую по длине пространствен­ную (объемную?) структуру (струну?), у которой попе­речное сечение тоже изменяемая, но равная по высоте и ширине, скрытая за индексацией величина.

В отличие от общепринятой системы координат, ин­дексация которой может содержать произвольный набор чисел, уравнение (2.9) составляется только из четырех иррациональных взаимосвязанных последовательных чисел русского ряда и по своему характеру является квантованной системой, т.е. качественно новым матема­тическим образованием. Возникает вопрос: Случайно ли получается квантованная координатная система? Или она может послужить основанием для построения кван­тованной геометрии? Для ответа на этот вопрос про­должим преобразования уравнения (2.9). Перенесем все ее индексы в правую часть и получим запись одинако­вую по форме как для динамической, так и для статиче­ской геометрии:

0 = п² – х² – у² – z². (2.10)

Рассматривая уравнение статической геометрии (2.10) Гильберт и Клейн предположили, что если приравнять п²= 1, то может существовать геометрия, в которой (2.10) имеет следующий вид:

0 ≠ 1² – х² – у² – z². (2.10′)

Поскольку правая часть уравнения не равна 0, то вме­сто 0 можно поставить s², и уравнение принимает вид:

s² = l² – x² – y² – z². (2.11)

Геометрия с таким основанием была названа псевдо­евклидовой геометрией. Именно ее использовал Минковский для введения «четвертого» измерения — време­ни t посредством приравнивания l² = с г:

s² = с²t² – х² – у² – z². (2.12)

И это уравнение (2.12), отображающее не четырех­мерный объем, а «рассечение» трехмерного простран­ства пятью плоскостями утвердилось в науке под на­званием «четырехмерный мир Минковского». Однако ни уравнение (2.11) ни (2.12) не являются аналогами урав­нений динамической геометрии (2.9) и (2.10), поскольку в них за координатной индексацией могут скрываться любые комбинации не связанных между собой чисел как рациональных, так и иррациональных (Например, квадрат произведения времени на скорость никак не связан с квадратами координатных осей.) А уравнения (2.9) и (2.10) образуются только иррациональными чис­лами любых трех последовательных чисел русского ря­да. Ни s ни п в данное уравнение, по-видимому, ввести невозможно, поскольку другие члены ряда не образуют соответствующих пропорций. И чтобы осуществить подстановку п в (2.10) так, чтобы получилось равенство вида п2 = 1² – s², необходимо «выйти» за пределы рус­ского ряда во вне, отыскать матрицу, содержащую поле взаимосвязанных иррациональных чисел и включаю­щую в свою структуру русский ряд. И такая матрица была найдена еще до рассмотрения данного ряда. Это русская матрица [28,30].

2.5. Структура русской матрицы

С русской матрицей мне пришлось познакомиться при изучении секретов старинных измерительных инстру­ментов — древнерусских саженей. Необъяснимой осо­бенностью этих инструментов являлось то, что их было много (десятки), они были несоизмеримы между собой, и при разметке объекта не допускалось разбиение осе­вых (координатных) размеров одной саженью. Разметка обязательно проводилась, начиная с высоты (координа­та – z) одной саженью, далее ширины (координата – х)— другой саженью и, наконец, длины (координата – у) — третьей саженью. Все оси разбивались только четным числом саженей. Было непонятно: зачем и как пользо­ваться десятками саженей, осложняя работу? Почему саженей много, разве нельзя обойтись одним измери­тельным инструментом? Почему они несоизмеримы между собой? Как могла сложиться такая архаичная система измерения? Почему она оставалась в употреб­лении в течение многих тысячелетий? И т. д. На эти многочисленные вопросы десятилетиями не находились ответы.

Однако А.А. Пилецкий [30] сумел свести все много­образие не пропорционированных друг другу древне­русских саженей к 15 типоразмерам, показать, что все они пропорциональны золотому числу Ф и подойти к построению матрицы, отражающей их взаимосвязи, ис­пользуя для этого применяемый только на Руси метод раздвоения-удвоения для получения из саженей более мелких измерительных инструментов. (По методу са­жень делилась надвое, получалось полсажени, полсаже­ни надвое — локоть и так далее до вершка. На вершке деление заканчивалось.) Именно метод раздвоения уд­воения привел к воссозданию русской матрицы (под­робнее [30, 31]). Приведу фрагмент русской матрицы (матрица 1).

Матрица 1.

9,609	8,643	7,774,	6.992	6,289	5,567	5,088	4,576	4,116	3,702	3,330
6,795	6,111	5,49"	4,944	4,447	4,000	3,598	3,236	2,911	2,618	2,355
4,804	4,321	3,88"	3,496	3,145	2,828	2,544	2,288	2,058	1,851	1,665
3,397	3,056	2,748	2,472	2,224	2,000	1,799	1,618	1,455	1,309	1,177
2,402	2,161	1,942	1,748	1,572	1,414	1,272	1,144	1,029	0,9256	0,8325
1,699	1,528	1,374	1,2361	1,112	1,000	0,8994	0,8090	0,7277	0,6545	0,5887
1,201	1,080	0,97170,8740	0,7861	0,7071	0,6360	0,5721	0,5145	0,4628	0,4163
0,8493	0,7693	0,6871 0,6180	0,5359	0,500	0,4497	0,4045	0,3638	0,3272	0,2943
0,6006	0,5402	0,4869 0,4370	0,3990	0,3536	0,3180	0,2860	0,2573	0,2314	0,2081
0,4247	0,3820	0,34360,3090	0,2779	0,2500	0,2249	0,2022	0,1819	0,1636	0,1472
0,3003	0,2701	0,24290,2185	0,1965	0,1768	0,1590	0,1430	0,1286	0,1157	0,1041

Основу структуры русской матрицы 1 составляет двойная крестовая последовательность записи чисел, при которой центр матрицы образует базисная 1 (еди­ница), и в одной с ней строке находятся цифры горизон­тального ряда, а перпендикулярно ей вертикальный (ба­зисный) ряд, формирующий числовое поле матрицы, начинающийся с рационального или иррационального числа. По диагонали через 1 снизу вверх слева направо — диагональный ряд, начинающийся либо с золотого числа Ф, либо Ф в степени, либо степень от него. Число­вое поле матрицы распространяется в бесконечность во все направления. Таким образом, матрицу формируют три числа:

• базисная 1, находящаяся в центре матрицы и на­личествующая во всех матрицах, иногда в виртуаль­ном виде;

• золотое число, следующее по диагонали от 1, как в виде Ф, так и Ф в степени или степень от него;

• рациональное или иррациональное число над 1 (кроме Ф).

Плоскость числового поля матрицы образуется как бы невидимыми квадратиками-клетками, в которые вписы­ваются числа.

Матрица 1, как и другие русские матрицы, имеет объ­емную слоистую структуру. Так, числа 1,414..., 1,272..., 1,144... и т.д., образуют ряд чисел, называемый также слоем, и заполняют слоями не только клетки вертикальной, видимой нами плоскости, но и те, которые сущест­вуют за ними и за данной плоскостью не наблюдаемы. В
створ им и за ними находятся пропорциональные им числа другого слоя-плоскости, еще дальше третьего и так далее в бесконечность.

Перед ними, т.е. в нашу сторону, виртуально, продол­жается такое же бесконечное поле взаимосвязанных и связанных с числами плоскости матрицы 1 числовых плоскостей. Их можно представить и по-другому, про­ведя через базисную 1 и другие числа горизонтального ряда горизонтальную плоскость-слой. Эта плоскость будет разграфлена такими же клетками, как и верти­кальная плоскость и в каждой клетке будут находиться числа, пропорциональные числам вертикального слоя и тоже пропорциональные Ф. То же произойдет и с гори­зонтальной плоскостью проведенной через числа 1,414; 1,272; 1,144 и т.д.

В результате клетки каждого слоя образуют единич­ные кубические объемы-ячейки, содержащие по одному иррациональному числу. И все числа бесконечного, объ­ема матрицы оказываются связанными между собой оп­ределенной числовой зависимостью. Далее речь пойдет в основном о вертикальных слоях матриц. Отмечу ос­новные особенности структуры русских матриц:

• плоскость матрицы имеет двойную крестовую структуру расположения чисел с центром в базис­ной 1;

• числовое поле матрицы объемно и бесконечно во все стороны;

• все члены любой части числового поля матрицы иррациональны, взаимосвязаны, но каждое число не равно никакому другому числу и по другую сторону базисной 1, оно имеет свой обратный аналог

• числовое поле плоской матрицы формируется тройкой чисел, а объемной матрицы —четверкой чисел. Количественные величины этих четырёх чисел позволяет образовывать бесчисленное количество матриц со свойствами золотых пропорций;

• базисная диагональ с числом пропорциональным Ф образуется по структуре аналогичной русскому или египетскому ряду;

• крестовая форма между столбцом и строкой мат­рицы обусловливает возможность использования их как координатные системы для нахождения мес­та любого числа ее множеств по показателю степе­ни строки иди столбца;

• базисный ряд может начинаться с любого числа как рационального, так и иррационального, но не может начинаться с Ф или ее элементов.

Структура русских матриц обладает множеством интересных свойств. Вот некоторые из них:

• Все последовательные тройки диагональных чисел матрицы 1 повторяют свойство русского ряда «плести гирлянду» подобных прямоугольников.

• Если в матрице 1 все числа каждой клетки возвести в квадрат, то получим матрицу 2, главная диагональ кото­рой будет структурирована египетским рядом.

• Тот же результат достигается и в том случае, если, на­чиная от базисной 1, и по горизонтали и по вертикали вычеркиваем через один столбец слои, начиная с числа 1,272..., и через строку, начиная с 1,414..., и оставшееся поле матрицы «сплачиваем», сдвигая слои к 1 (матрица 2). Если же вычеркивать слои и столбцы через строку, начиная с крестовины базисной 1, и сплотить оставшее­ся поле матрицы, то получим матрицу, обладающую те­ми же свойствами, но с виртуальной 1.

• Последовательность диагональных чисел матрицы 2 после сплочения из матрицы 1, «теряют» способность образовывать «гирлянды» треугольников, но у них ярко проявляется достаточно скрытая в других формах матриц качество матричной «вязи», заключающееся в возмож- ности получения методом сложения или вычитания из одних чисел других, находящихся в том же поле.

Приведу несколько примеров матричной вязи, опира­ясь на известное правило сложения и вычи­тания Фибоначчи. Напомню его и покажу еще некото­рые из них на примере числового поля, окружающего базисную 1, отметив, что в примерах она базисной не принимается, поскольку по той же конфигурации могут складываться любые числа поля [30].

Получаем базисную 1, соблюдая правило Фибоначчи, когда сумма двух последовательных нижних чисел по диагонали слева направо снизу вверх равна верхнему числу. Те же числа находятся при диагональном вычи­тании из верхнего любого из двух нижних чисел:

Матрица 2

283.3	229,2	184,7	149,4	120,9	98,78	79,11	60,0	51,77	41,89	33,89
141,8	114,4	92,33	74,70	60,43	48,89	39,55	32,0	25,89	20,94	16,94
70,85	57,31	46,17	37,35	30,22	24,44	19,78	16,0	12,94	10,47	8,472
35,42	28,66	23,08	18,67	15,11	12,22	9,888	8,00	6,472	5,236	4,236
17,71	14,33	11,54	9,337	7,554	6,114	4,944	4,00	3,326	2,618	2,118
8,854	7,164	5,771	4,668	3,777	3,058	2,472	2,00	1,618	1,309	1,059
4,427	3,582	2,885	2,334	1,888	1,528	1,236	1,00	0,809	0,6545	0,5295
2,214	1,791	1,449	1,167	0,944	0,764	0,618	0,50	0,4045	0,3272	0,2643
1,107	0,8955	0,7214	0,5836	0,472	0,382	0,309	0,25	0,2023	0,1636	0,1324
0,5534	0,4477	0,3607	0,2920	0,236	0,191	0,1545	0,125	0,1011	0,0818	0,0662
0,2767	0,2239	0,1803	0,1460	0,118	0,0955	0,0772	0,0625	0,0506	0,0409	0,0331
0,1383	0,1119	0,0902	0,0730	0,059	0,0478	0,0386	0,0313	0,0253	0,0204	0,0165
0,0692	0,0560	0,0451	0,0365	0,0295	0,0239	0,0193	0,0156	0,0126	0,0102	0,0083
0,0340	0,0280	0,0225	0,0182	0,0148	0,0119	0,0096	0,0073	0,0063	0,0051	0,0041

0,382 + 0,618 =1.

Складывая по диагонали вверх три числа подряд, по­лучаем в результате число, стоящее в таблице над по­следним слагаемым:

0,382 + 0,618 +1 = 2.

Берем число 0,191, стоящее в таблице под 0,382. И складываем его методом единицы (движение по полю матрицы как бы выписывает единицу) с числом 0,809, находящимся от него через два числа вверх вправо по диагонали. Результат сложения находится слева от чис­ла 0,809:

0,191 + 0,809 =1.

Используем метод двойного хода "шахматного коня": с поля 0,236 "переступаем" через число 0,472, а от числа 0,944 движемся направо к 0,764 и складываем его с пер­вым:

0,236 + 0,764 =1.

"Шаги" через числа могут быть и более длинными. Например, возьмем число 0,056 на главной диагонали. Через пять чисел вверх на числе 1,783 повернем вправо и через два числа найдем, 0,944. Сложим их, сделав один шаг наверх и два вправо, находим 1:

0,056 + 0,944 =1.

Или, по тем же правилам, от числа 0,118 пройдем к числу 2 и, сделав ход вверх и два вправо, имеем:

0,118 + 2 = 2,118.

Или по главной диагонали:

0,0213 + 0,0344 + 0,0902 + 0,236 + 0,618 =1.

Количество слагаемых может возрастать. Например, суммируя числа главной диагонали 0,146; 0,382, с числом 1, получить результат 1,528 находящийся через число вле­во от 1:

0,146 + 0,382 +1 = 1,528,

оставаться последовательным:

0,146 + 0,382 + 0,472 =1,
становиться фрактальным:

0,1803 + 0,236 + 0,5836 = 1,

или образовывать различные комбинации из них:

0,08514 + 0,1114 + 0,146 + 0,2755 + 0,382 = 1. И т.д.

Количество примеров можно множить и множить. Правила их использования относятся ко всем числам поля и в совокупности со степенными числовыми ряда­ми образуют матричную «вязь», охватывающую все числовое поле как матрицы 1, так и матрицы 2. Именно матричная «вязь» обеспечивает корректность операций между золотыми числами полей этих матриц.

Приведу еще один вариант матрицы, связанный как с древнерусскими саженями, так и с размерностью физи­ческих уравнений. Начну с саженей. Оказалось, что длины древних саженей были извлечены из числового поля матрицы, в которой число, задающее шаг базисно­го столбца, является малой темперированной секундой музыкального ряда, равной 1,05945... и получается из­влечением корня двенадцатой степени из 2, главная диа­гональ кратна Ф, а сама матрица имеет гармоническую структуру, относящуюся не только к музыке, но и са­мым непосредственным образом к физике. Числа базисного ряда гармонической матрицы 3 являются качест­венными коэффициентами физической размерен-ности (КФР) свойств тел, основой теории размеренности. КФР позволяет принципиально по-иному подходить к этой теории и к формализации физических уравнений (ниже метод КФР будет разобран подробнее). Приведу фрагмент матрицы 3.

Матрица 3

0,1670 0,2550 0,3895 0,5949 0,9085 1,387 2,119 3,236 4,942

0,1576 0,2407 0,3676 0,5615 0,8575 1,309 2,000 3,054 4,665

0,1488 0,2272 0,3470 0,5300 0,8094 1,236 1,888 2,883 4,403

0,1404 0,2146 0,3275 0,5002 0,7639 1,167 1,782 2,721 4,156

0,1325 0,2024 0,3091 0,4721 0,7211 1,101 1,682 2,568 3,923

Дата добавления: 2014-11-29