
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Тема 1. Предел функции
|
|
|
|
ВВНЧ1/Э1ВШ.СШВО ХВХ ВХШОЛВ^Зи ЬеНЯ1/ВИ^100
Г^ЕОО- 169-5 N951
I г/ЕООи 16958^||6
•эеЛа кю>1ЭЭьи_1(Х1вНэи а нншшиТшН
иоле винвавИоиэс1и Ляшявйи окхшэишонп
иэТпопйлдодо 'шин» 1яс1о18В.Ю1В^цИЭ(1и
эшонм и И1е вн 1/вшеа иоаэ ^шхнчуэхваУ ио)IЭЭьи^о^еVЭи-он^^леиТ10э вшоионхэх и
И1ЭОНЧ1/Э1ВЭ1Г ИОНЧ1ШНОИЭЭ9фОС1и В)1ИфиГ1ЭиЭ
эихв» ^иювхАвн и^шАй/ и иэи-шохиэи
'иэи-кмоиГюо 'иохи.кх]й/эи о внвеваэ вно хех
^ихАвн иоле 1эм1/э(1и и 1»эядо аохв» 'аохэаю
хнньвнеонй'о 1^эь 'аоэойиоа хянноиээАхэий1
этя!/од о^евс1о^ чнэй1 иингшнНсиээ вн
эхАвн И016 а 01Ь 'оня1/Э1иа^Аэн
ииээос! а И1ЭОНЯ1/Э1ВЭ1/ ионяивноиэээфос!и вйэфо и винвне о^ннАвн Я1эв(/до
Число А называется пределом функции 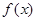 при
при 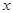 , стремящимся к
, стремящимся к  , если для любого положительного числа
, если для любого положительного числа 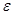 (
(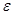 >0) найдется такое положительное число
>0) найдется такое положительное число  >0 (зависящее в общем случае от
>0 (зависящее в общем случае от 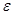 ), что для всех
), что для всех 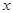 , не равных
, не равных  и удовлетворяющих условию x
и удовлетворяющих условию x 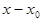 x<
x<  , выполняется неравенство x
, выполняется неравенство x 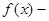 А x<
А x< 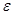 .
.
Для предела функции вводится обозначение 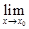
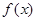 =А.
=А.
Пределы функций обладают следующими основными свойствами:
Функция не может иметь более одного предела.
Если 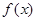 = С (постоянная), то
= С (постоянная), то 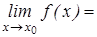 С.
С.
Если существует 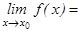 А, то для любого числа
А, то для любого числа 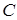 верно:
верно:
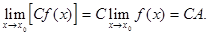
Если существуют 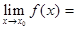 А и
А и 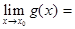 В, то
В, то 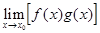 =
= 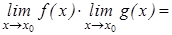 АВ,
АВ, 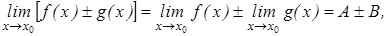 а если В
а если В 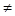 0, то
0, то
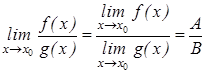 .
.
Операция предельного перехода перестановочна с операцией вычисления непрерывной функции, т. е. справедлива формула 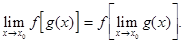
Если функция 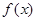 непрерывна в точке
непрерывна в точке  , то искомый предел равен значению функции в этой точке, т.е. он находится непосредственной подстановкой предельного значения переменной вместо аргумента
, то искомый предел равен значению функции в этой точке, т.е. он находится непосредственной подстановкой предельного значения переменной вместо аргумента 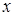 :
: 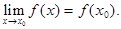
Функция 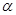 (
(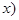 называется бесконечно малой величиной при
называется бесконечно малой величиной при 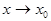 , если ее предел равен нулю:
, если ее предел равен нулю: 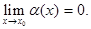 Функция
Функция 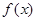 называется бесконечно большой величиной при
называется бесконечно большой величиной при 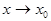 , если
, если 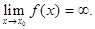
Пример 1. 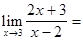
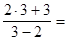
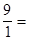 9.
9.
Пример 2. 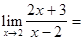
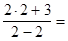
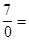
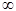 .
.
В рассмотренных примерах предел находился сразу: в виде числа или символа 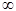 (бесконечность). Но чаще при вычислении пределов мы встречаемся с неопределенностями, когда результат нахождения предела не ясен, например, в случае отношения двух бесконечно малых функций (условное обозначение
(бесконечность). Но чаще при вычислении пределов мы встречаемся с неопределенностями, когда результат нахождения предела не ясен, например, в случае отношения двух бесконечно малых функций (условное обозначение 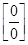 ) или бесконечно больших (
) или бесконечно больших ( ).Кроме названных встречаются неопределенности вида
).Кроме названных встречаются неопределенности вида 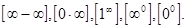
Для раскрытия неопределенностей используются специальные приемы и два следующих предела, которые играют особую роль в математике и поэтому называются замечательными:
- первый замечательный предел 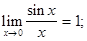
-второй замечательный предел 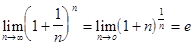 (число Эйлера).
(число Эйлера).
Пример 3. 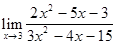 .
.
Решение. Непосредственной подстановкой убеждаемся, что имеем дело с неопределенностью вида 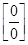 :
:
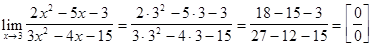 .
.
Для раскрытия неопределенности разложим числитель и знаменатель на множители. Найдем корни многочлена, стоящего в числителе. Для этого составим уравнение второй степени 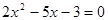 и найдем его решение:
и найдем его решение:
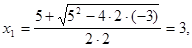
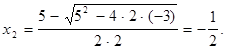
Тогда для квадратного трехчлена справедливо разложение на множители
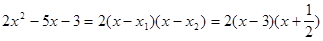 .
.
Аналогичные действия выполним для многочлена, стоящего в знаменателе.
Уравнение 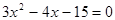 имеет решения
имеет решения
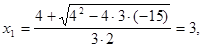
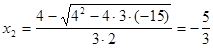
и знаменатель представляется в виде: 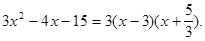
Сократим дробь на множитель 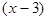 и вычислим ее при
и вычислим ее при 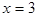
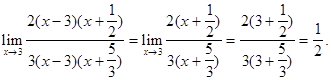
Пример 4. 
Решение. Непосредственной подстановкой убеждаемся, что возникает неопределенность вида 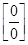 . Для раскрытия неопределенности умножим числитель и знаменатель на выражение
. Для раскрытия неопределенности умножим числитель и знаменатель на выражение 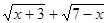 , являющееся сопряженным к знаменателю
, являющееся сопряженным к знаменателю
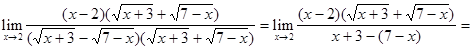
= 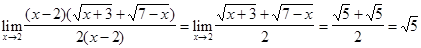 .
.
Пример 5. 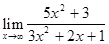 .
.
Решение. Имеем неопределенность вида  . Разделим числитель и знаменатель на
. Разделим числитель и знаменатель на 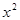 (в более общем случае, когда числитель и знаменатель представляют многочлены разных степеней, делят на
(в более общем случае, когда числитель и знаменатель представляют многочлены разных степеней, делят на 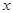 с наибольшим показателем степени числителя и знаменателя). Используя свойства пределов, получим:
с наибольшим показателем степени числителя и знаменателя). Используя свойства пределов, получим:
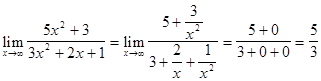 .
.
Пример 6. 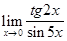 .
.
Решение. При 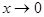 имеем неопределенность вида
имеем неопределенность вида 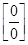 . Представим
. Представим 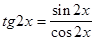 , разделим и умножим числитель и знаменатель на числа 2, 5 и
, разделим и умножим числитель и знаменатель на числа 2, 5 и 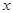 , тогда предел преобразуется к виду:
, тогда предел преобразуется к виду:

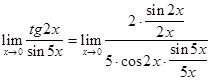 .
.
Пользуясь свойствами пределов и первым замечательным пределом, далее имеем:
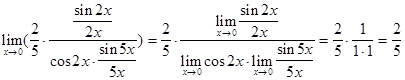 .
.
Пример 7. 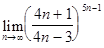 .
.
Решение. Имеем неопределенность вида [ 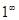 ], так как
], так как
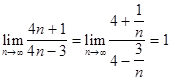 , а
, а  .
.
Выделим у дроби целую часть
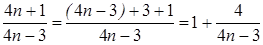 .
.
Введем новую переменную 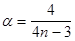 и выразим отсюда
и выразим отсюда 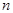 через
через 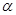 :
: 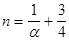 . Тогда
. Тогда
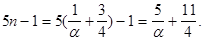
Заметим, что при 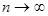 переменная
переменная 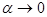 . Теперь, переходя к новой переменной и используя второй замечательный предел, получим:
. Теперь, переходя к новой переменной и используя второй замечательный предел, получим:
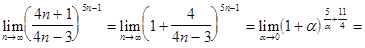
= 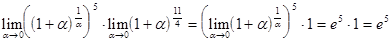 .
.
Неопределенности вида 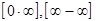 путем алгебраических преобразований приводятся к виду
путем алгебраических преобразований приводятся к виду 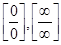 . Неопределенности вида
. Неопределенности вида 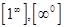 ,
, 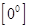 можно раскрыть, предварительно прологарифмировав соответствующую функцию. Неопределенности вида
можно раскрыть, предварительно прологарифмировав соответствующую функцию. Неопределенности вида 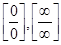 можно исключить, используя правило Лопиталя, которое изложено в конце темы 2.
можно исключить, используя правило Лопиталя, которое изложено в конце темы 2.
Пример 8. Первоначальный вклад в банк составил 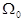 денежных единиц. Банк выплачивает ежегодно
денежных единиц. Банк выплачивает ежегодно 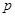 % годовых. Необходимо найти размер вклада
% годовых. Необходимо найти размер вклада 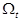 через
через 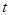 лет при непрерывном начислении процентов. Решить задачу при
лет при непрерывном начислении процентов. Решить задачу при 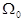 =10,
=10, 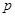 =5%,
=5%, 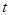 =20 лет.
=20 лет.
Решение. При 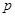 % годовых размер вклада ежегодно будет увеличиваться в
% годовых размер вклада ежегодно будет увеличиваться в
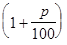 раз, т.е.
раз, т.е. 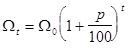 .
.
Если начислять проценты по вкладам не один раз в год, а 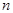 раз, то размер вклада за
раз, то размер вклада за 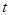 лет при
лет при 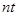 начислениях составит
начислениях составит
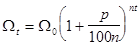 .
.
Тогда размер вклада за 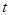 лет при непрерывном начислении процентов (
лет при непрерывном начислении процентов (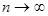 ) сводится к нахождению предела
) сводится к нахождению предела
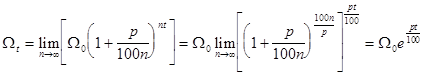 .
.
Здесь при решении использовался второй замечательный предел.
Подставляя исходные числовые данные задачи, получаем
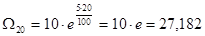 (ден. единиц).
(ден. единиц).
Вопросы для самопроверки
Дайте определение предела функции в точке.
Назовите основные свойства пределов функций.
Какие виды неопределенностей встречаются при нахождении пределов?
Какие пределы называются замечательными?
Какие функции называют бесконечно малыми?
Задачи для самостоятельной работы
Найти пределы следующих функций:
| Номер варианта | А) | Б) |

| 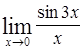
| |
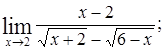
| 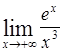
| |
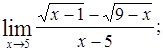
| 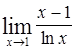
| |
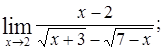
| 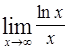
| |

| 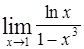
| |
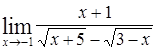
| 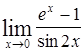
| |
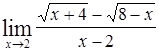
| 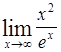
| |
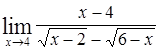
| 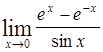
| |
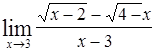
| 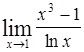
| |
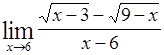
| 
|
Таблица 1.
|
|
|
|
|
Дата добавления: 2014-12-17; Просмотров: 450; Нарушение авторских прав?; Мы поможем в написании вашей работы!