Тема 2. Производная функции

Приращением функции 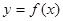в точке 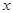, соответствующим приращению аргумента 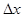, называется число .

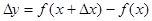Производной функции 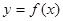в точке называется предел отношения приращения функции 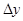к приращению аргумента 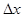при 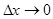, если этот предел существует, и обозначается:

.

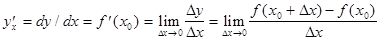Нахождение производной функции называется дифференцированием этой функции. Если функция 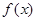имеет в точке конечную производную, то функция называется дифференцируемой в этой точке.

Важнейшими правилами дифференцирования являются следующие.

Производная постоянной 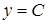равна нулю: .

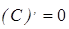Постоянный множитель выносится за знак производной

.

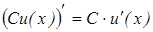Производная суммы (разности) функций равна сумме (разности) производных этих функций

.

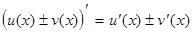Производная произведения двух дифференцируемых функций равна произведению производной первого сомножителя на второй плюс произведение первого сомножителя на производную второго

.

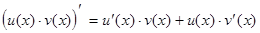Производная частного двух дифференцируемых функций находится по формуле

.

Пусть переменная 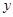есть функция от переменной 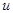(например, 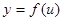), а переменная 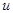, в свою очередь, есть функция от независимой переменной 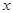(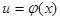), иначе задана сложная функция .

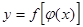Есл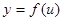и и 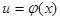- дифференцируемые функции от своих аргументов, то производная сложной функции существует и равна производной данной функции по промежуточному аргументу 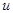, умноженной на производную самого промежуточного аргумента по независимой переменной :

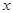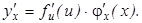
Если функция, производную которой нужно найти, представляет из себя комбинацию элементарных функций, то для вычисления производной применяются правила дифференцирования и таблица производных элементарных функций, приводимая ниже.

Таблица 2.

№	функция	производная	№	функция	производная
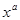
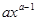
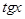
					1/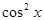
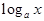
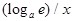
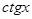
					-1/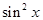
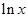
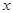
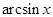
		1/			1/()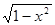
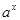
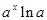
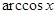
					-1/()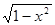
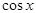
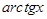
					1/(1+ )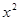
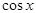
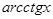
		-			-1/(1+ )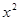

Пример 1. Найти производную функции

.

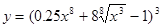Решение. Представим ее как сложную функцию. Пусть 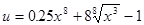, тогда 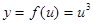и 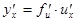. Найдем производную по промежуточному аргументу 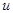как степенной функции

.

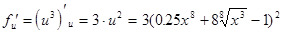В свою очередь, промежуточный аргумент 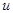представляется в виде суммы двух степенных функций минус постоянная, поэтому, используя правила 1-3,по-лучим

= .

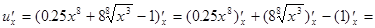
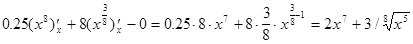Отсюда производная искомой функции

.

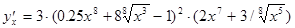Пример 2. Найти производную функции

.

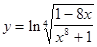Решение. Обозначим 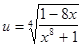, 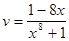. Тогда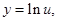 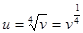и искомая производная находится из формулы .

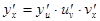Производную 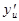находим из таблицы производных элементарных функций

.

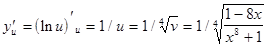Второй сомножитель 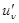представляет производную от степенной функции

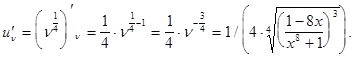
Наконец, последняя производная 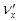находится по правилам дифференцирования частного

= = .

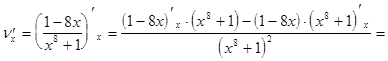
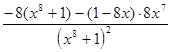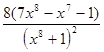В итоге получаем искомую производную

.

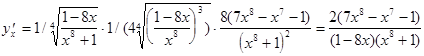Пример 3. Наити производную

.

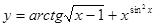Решение. Производная суммы двух функций есть сумма их производных

.

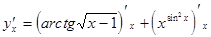Для нахождения производной первого слагаемого 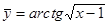обозначим , .

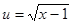Тогда ,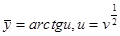

=

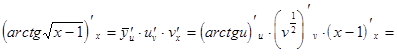
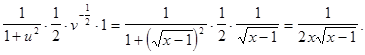
Производную второго слагаемого 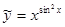найдем по правилу дифференцирования степенно-показательной функции. Прологарифмируем функцию 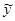: 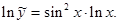Дифференцируем левую и правую часть полученного равенства

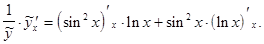
Отсюда

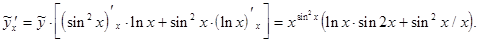
Наконец, находим производную искомой функции

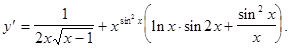
Пример 4. На основе опытных данных построена математическая модель спроса 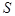населения на некоторый товар в зависимости от цены :

.

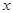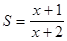Определить эластичность спроса при 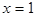(в условных денежных един.).

Решение. Эластичностью спроса называют предел отношения относительного приращения спроса 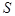к относительному приращению цены 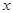при :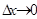

.

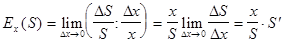Если 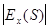>1, то спрос называют эластичным, при 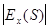<1 – неэластичным, а при 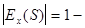нейтральным.

Найдем производную

.

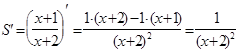Тогда

.

Определим эластичность спроса при 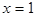: 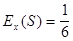. Таким образом, при такой цене имеем неэластичный спрос.

Правило Лопиталя. При нахождении пределов функций (тема 1) неопределенности вида 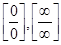можно исключить, применяя правило Лопиталя: предел отношения двух бесконечно малых или бесконечно больших функций равен пределу отношения их производных, если последний существует, т. е.

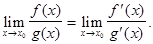
Ес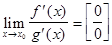ли (или ), то правило Лопиталя можно использовать вторично, т.е.

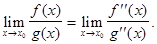
В общем случае правило Лопиталя можно применять неоднократно.

Пример 5. Найти

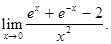
Решение. Для раскрытия неопределенности применим правило Лопиталя.

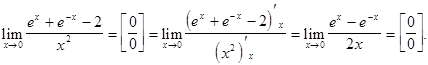
Неопределенность вида 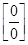по-прежнему сохраняется. Применим правило Лопиталя еще раз:

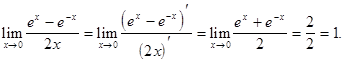
Вопросы для самопроверки

Дайте определение производной функции в точке.

Какая функция называется дифференцируемой в точке?

Назовите важнейшие правила дифференцирования.

Как находится производная сложной функции?

Сформулируйте правило Лопиталя.

Задачи для самостоятельной работы

Найти производные следующих функций:

Таблица 3.

Номер варианта	А)	Б)	В)
	y=(3x4-4x(-1/4)+2)5	y=arccos2x+(1-4x2)1/2	y=2tgx+x sin(2x
	y=(5x2+4x(5/4)+3)3	y=arctg(x2-1)1/2	y=e3x-2x tg(3x)
	y=(0.25x8+8x(3/8)-1)3	y=arccos(1-x2)1/2	y=3cosx-x sin(2x)
	y=(0.2x5-3x(4/3)-4)4	y=arctg(x-1)1/2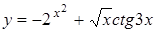
	y=(3x8+5x(2/5)-3)5	y=arctg(2/(x-3))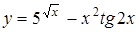
	y=(5x4-2x(-3/2)+3)4	y=arccos(1-x)1/2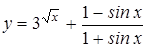
	y=(4x3+3x(-4/3)-2)5	y=arcctg(x-1)1/2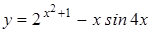
	y=(7x5-3x(5/3)-6)4	y=arcsin3x-(1-9x2)1/2	y=etgx-x1/2 cos(2x).
	y=(3x4-4x(-1/4)-3)5	y=arctg(1/(x-1))	y=x tg3x+2x-2
	y=(8x3-9x(-7/3)+6)5	y=arcsin((1-x)1/2)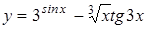

Дата добавления: 2014-12-17