Тема 5. Неопределенный интеграл

Функция 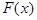называется первообразной функцией для функции 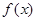, заданной на интервале 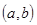, если в каждой точке этого интервала функция 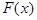дифференцируема и имеет производную 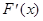, равную 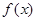, т.е.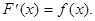

Отсюда следует, что если 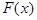-первообразная для функции 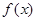,то выражение вида 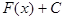, где C - произвольное число, также является первообразной для .

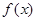Совокупность всех первообразных функций для данной функции 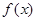на интервале 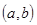называется неопределенным интегралом от функции 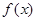и обозначается символом 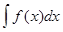, где 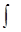-знак интеграла, 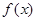-подынтегральная функция, 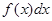-подынтегральное выражение.

Если 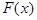-одна из первообразных для 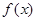на интервале 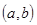, то

,

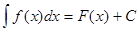где 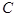-произвольная постоянная.

Операция нахождения неопределенного интеграла от некоторой функции называется интегрированием этой функции. Отметим основные свойства неопределенного интеграла.

Производная от неопределенного интеграла равна подынтегральной функции, т.е.

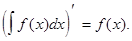
Неопределенный интеграл от дифференциала некоторой функции равен этой функции с точностью до постоянного слагаемого, т.е.

.

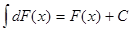Постоянный множитель можно выносить за знак интеграла

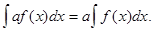
Интеграл от алгебраической суммы двух функций равен такой же сумме интегралов от этих функций в отдельности

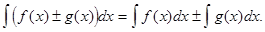
Основу вычислительного аппарата интегрального исчисления составляет таблица неопределенных интегралов от основных элементарных функций, приводимая ниже.

Таблица 7.

№ пп	Подынт. функция	Неопределенный интеграл	№ пп	Подынт. функция	Неопределенный интеграл
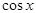
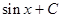
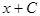
				1/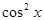
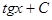
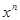
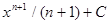
				1/	-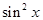
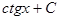
	1/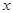

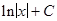
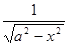
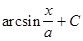
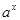
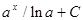
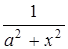
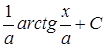
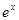
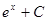
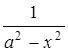
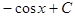
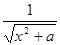
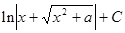
Пример 1. Найти интеграл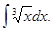

Решение. Воспользуемся табличным интегралом от степенной функции (п.3 в таб.7) для

:

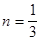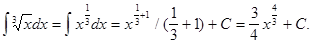
Проверим правильность вычисления дифференцированием правой части

.

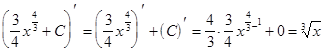Получена подынтегральная функция, что говорит о правильном нахождении неопределенного интеграла.

При вычислении неопределенных интегралов приведенную таблицу дополняют специальными приемами и методами интегрирования, два из которых рассмотрены ниже.

Интегрирование заменой переменной (подстановкой)

Замена переменной – один из самых эффективных приемов интегрирования, который основывается на следующем.

Пусть требуется найти В ряде случаев удается выбрать в качестве новой переменной такую дифференцируемую функцию 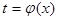, что имеет место равенство 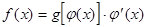, причем функция 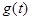легко интегрируется, т.е.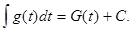

Тогда

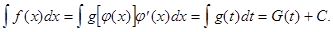
Удачная замена переменной позволяет упростить исходный интеграл и в ряде случаев свести его к табличному.

Пример 2. Найти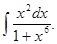

Решение. Положим 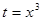. Тогда 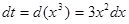. Умножим и разделим исходный интеграл на число 3 и выполним следующие преобразования

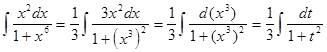
Полученный интеграл относится к табличным и, следовательно,

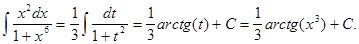
Сделаем проверку дифференцированием:

.

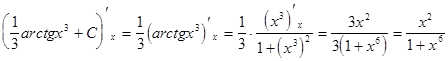Полученная производная совпадает с подынтегральной функцией исходного

интеграла, что говорит о правильности вычислений.

Пример 3. Вычислить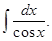

Решение. Чтобы выявить замену, посредством которой может быть вычислен этот интеграл, преобразуем его к виду

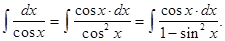
Если положить 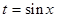, тогда 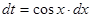и в результате получим

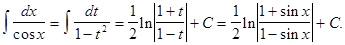
Интегрирование по частям

Этот метод основывается на следующем утверждении. Пусть функции дифференцируемы и существует первообразная для функции 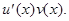Тогда существует первообразная и для функции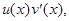

причем справедлива формула

,

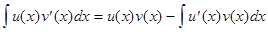называемая формулой интегрирования по частям.

Пример 4. Найти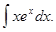

Решение. Положим 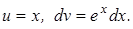Тогда

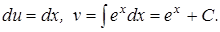
Произвольную постоянную 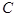в этих случаях исключают и записывают

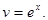Теперь, применяя формулу интегрирования по частям, получим

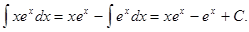
Иногда формулу интегрирования по частям приходится применять неоднократно.

Пример 5. Вычислить

Решение. Полагая 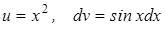, имеем

, .

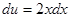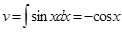Применяя формулу интегрирования по частям, получим

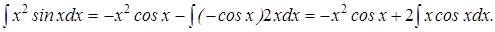
Степень переменной 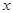в подынтегральном выражении уменьшилась на единицу. Повторим применение формулы интегрирования по частям. Поло-

жим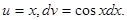

Отсюда

Тогда

+

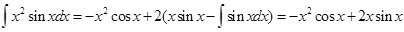Вопросы для самоконтроля

Дайте определение первообразной функции.

Что называют неопределенным интегралом?

Перечислите основные свойства неопределенного интеграла.

В чем суть приема, называемого заменой переменной?

На чем основан метод интегрирования по частям?

Задачи для самостоятельной работы

Найти неопределенные интегралы, результаты проверить дифференцированием:

Номер варианта	А)	Б)

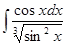
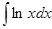
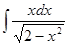
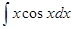
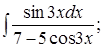
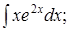
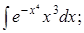
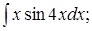
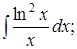
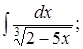
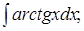
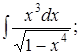
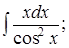
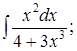
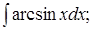
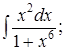
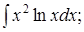
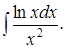
Дата добавления: 2014-12-17