Ранг матрицы. Определение и свойства

Опр. 11.1. Ранг системы векторов векторов столбцов матрицы А как векторов арифметического пространства P^m, наз. рангом матрицы А и обозначается rang(A) или rangA.

Опр. 11.2. Пусть 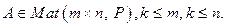Если в матрице А выделить k строк и k столбцов, то на их пересечении будет стоять матрица размера Определитель этой матрицы называется минором k-го порядка матрицы А (стоящим в выбранных k-строках и k-столбцах).

Опр. 11.3. Если в матрице А все миноры k-го порядка равны 0, то все миноры порядка больше, чем k, также равны нулю. Доказательство: Пусть в матрице А все миноры k-го порядка равны нулю. Рассмотрим произвольный минор порядка k+1. По теореме о разложении определителя по элементам строки, этот определитель равен сумме произведений , 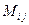- миноры k-го порядка матрицы. ■

Св-во 11.4. Если у матрицы А все миноры k-го порядка =0, то и у матрицы А^Т все миноры k-го порядка =0. Доказательство. Любой минор k-го порядка матрицы А^Т транспонируем, к соответствующему минору матрицы А, т.к. 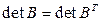, то он равен нулю. ■

Лемма 11.5. Если у матрицы А в левом верхнем углу стоит минор порядка 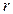, 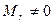. А все миноры порядка 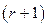матрицы А равны нулю, то тогда 1) система первых r-столбцов матрицы А лин. независ.
2)

3) .

4)

5) . Доказательство: , ,

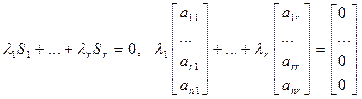(*) – это однородная система 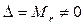по условию следует, что это система имеет 1 решение: 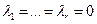, значит столбцы - лин. независ.

П2. Если , то определитель содержит 2 равные строки или 2 равных столбца. По св-ву определитель равен нулю. Если , то определитель равен нулю по условию. П3. Раскладываем определитель 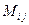по последней строке и получаем требуемое равенство. П4. следует из П3., П5. иная формулировка П4. ■

Замечание 11.6. Тот факт, что в 11.5 определитель 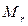строки в левом верхнем углу, т.е. в первых r-строках и первых r-столбцах. Объясняется только удобством записи, т.е. это мог бы быть любой минор порядка 5.

Следствие 11.7. Наибольший из порядков миноров матрицы А не равных 0, равен рангу матрицы А. Доказательство: Возьмем этот минор 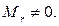В пункте 1 леммы доказано, что столбцы, в которых стоит этот минор, линейно независимые. А из пункта 5 следует, что если к этим столбцам приписать любой столбец, получим линейно зависимую систему из столбцов. Значит это R-столбцов – это МЛНП матрицы А. Значит ранг А=R. ■

Опр 11.8. Ранг системы столбцов матрицы А равен рангу системы строк.

Следствие 11.10. 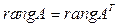- переформулировка 11.9.

Следствие 11.11. Пусть 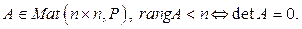Доказательство. В А существует только 1 минор n-го порядка – это определитель матрицы А. По следствию 11.7. получаем , с другой стороны или , то не равный нулю минор наибольшего размера имеет размер меньше n. Значит ■

Следствие 11.12. один из столбцов матрицы А линейно выражается через остальные ее столбцы. Доказательство: 1) если А=0_nxn – очевидно. 2) если один из столбцов матрицы А линейно выражается ч/з остальные по св-ву определителя . Наоборот: Пусть . По 11.11. ранг матрицы А равен r<n. Значит МЛНП системы столбцов содержит r-столбцов. Вся система выражается через МЛНП. Тогда тот столбец, который не входит в МЛНП выражается в МЛНП, значит через остальные столбцы. ■

Опр. 11.13. Пусть 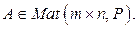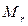- некоторый минор А. В дополнение к выделенным r-строкам и r-столбцам выделим еще одну строку и столбец. Получим минор 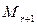, который наз. окаймляющим минора .

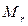Теорема 11.14. Пусть 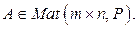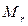- ненулевой минор матрицы А, а все окаймляющие 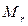миноры равны 0. Тогда ранг матрицы А=r. Доказательство: Из леммы 11.5 с учетом 11.6 и 11.12 следует, что все миноры (k+1) порядка матрицы А равны нулю. Тогда по 11.7 ■

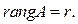Опр. 11.16. Элементарными преобразованиями матрицы А наз. 1) умножение строки или столбца на ненулевой скаляр. 2) прибавление к строке или столбцу другой строки или столбца, умноженного на скаляр. 3) приписывание к матрице нулевых строк или столбцов, а также вычеркивание нулевых строк или столбцов.

Теорема 11.17. При элементарных преобразованиях ранг матрицы не изменяется.

Доказательство. Ранг матрицы – это ранг системы столбцов и ранг системы строк, а элементарные преобразования матрицы – это элементарные преобразования либо системы строк, либо системы столбцов. По 11.5 и 11.6 ранг системы векторов не изменяется при элементарных преобразованиях. ■

Дата добавления: 2014-11-29