Волновая функция

Какова природа волн де Бройля? Это не электромагнитные волны. Электромагнитные волны представляют собой распространяющееся в пространстве переменное электромагнитное поле. Распространение же волн де Бройля не связано с распространением в пространстве какого-либо электромагнитного поля. Можно сказать, что волны де Бройля имеют специфическую квантовую природу, не имеющую аналогии с волнами в классической физике.

Запишем волновое уравнение плоской гармонической волны, распространяющейся вдоль оси x,

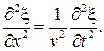(80.1)

Его решение

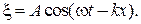(80.2)

Используя формулу Эйлера

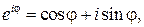
запишем выражение (80.2) в виде

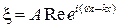
или (опуская знак Re — реальная часть)

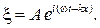(80.3)

Рассмотрим микрочастицу, свободно движущуюся вдоль оси x. Согласно де Бройлю, ей нужно сопоставить плоскую волну

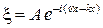(80.4)

(в квантовой механике принято показатель экспоненты брать со знаком минус).

Запишем выражение для энергии и импульса микрочастицы

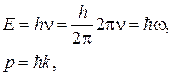
откуда

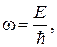(80.5)

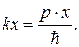(80.6)

Подставляя формулы (80.5) и (80.6) в выражение (80.4), получаем

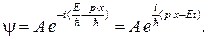(80.7)

Функцию 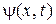называют волновой функцией, или пси-функцией.

В опыте Дэвиссона и Джермера обнаруживается неодинаковое распределение пучка электронов, отраженных от кристалла, по различным направлениям, а именно, в некоторых направлениях наблюдается большее число электронов, чем в других. С волновой точки зрения, наличие максимумов числа электронов в некоторых направлениях означает, что эти направления соответствуют наибольшей интенсивности I волн де Бройля. Можно сказать, что интенсивность I волн де Бройля в данной точке пространства определяет плотность вероятности попадания электронов в эту точку.

Обозначим через dP вероятность нахождения микрочастицы в элементарном интервале dx оси x. Так как в вакууме интенсивность волны I = A ², где A — амплитуда волны, то плотность вероятности нахождения микрочастицы в точке с координатой x (в пределах интервала dx)

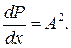(80.8)

Из выражения (80.7) следует

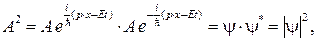(80.9)

где φ и φ^* — величины комплексно сопряженные. С учетом выражения (80.9) запишем соотношение (80.8)

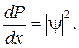(80.10)

Из соотношения (80.10) следует, что квадрат модуля волновой функции 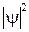имеет смысл плотности вероятности нахождения микрочастицы в точке с координатой x в пределах элементарного интервала координат dx.

Если мы знаем 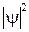в каждой точке оси x, то вероятность нахождения микрочастицы в интервале координат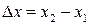

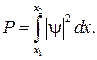(80.11)

Если микрочастица локализована только в этом интервале координат 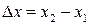, то вероятность нахождения микрочастицы в этом интервале равна единице:

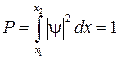(80.12)

— условие нормировки вероятности.

Дата добавления: 2014-11-29