Кинетика и термодинамика в описании процесса роста при молекулярно-пучковой эпитаксии

На первом этапе исследований (конец 70-х-начало 80-х годов прошлого века) преобладало мнение, что МПЭ является сугубо неравновесным процессом, т.к. вещества, поступающие на подложку и продукты реакции, в общем случае, имеют разные температуры. Поэтому термодинамические представления считались неприменимыми, а информацию о процессах роста предполагалось получать только путем исследования кинетики конкретных реакций на поверхности. На основе экспериментов с модулированными пучками были развиты представления, согласно которым основную роль при МПЭ соединений А^IIВ^VI (А^IIIB^V) играют элементарные процессы адсорбции, миграции, встраивания и десорбции атомов и молекул, а также разложение кристалла (рис. 6) [10]. Исследование этих процессов, протекающих на поверхности растущего слоя имеют не только фундаментальное значение, но также и огромную практическую значимость, связанную с дополнительными возможностями in situ контроля процесса роста эпитаксиальных слоев и гетероструктур. Сегодня интенсивно ведутся экспериментальные исследования поверхности с использованием широкого спектра различных методик, таких как ДБЭ, встроенная СТМ, лазерная интерферометрия и др.

Среди теоретических подходов, применяемых для описания и моде­лирования эпитаксиального роста соединений A^IIIB^V и А^IIВ^VI следует

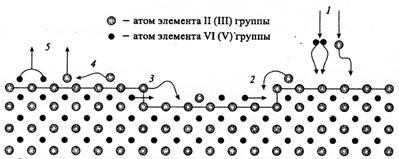
Рис. 6. Схематическое изображение основных процессов на подложке:

1 — адсорбция; 2 — встраивание; 3 — разложение; 4 — миграция; 5 — десорбция

прежде всего выделить метод Монте-Карло. Этот метод позволяет воспроизвести экспериментальные данные, но требует «а priori» опре­деления большого числа параметров, которые могут быть лишь прибли­зительно оценены из первых принципов. В такой ситуации чрезвычайно актуальными являются упрощенные кинетические модели, содержащие минимальное число параметров. В основе большинства моделей зало­жено предположение, что все процессы протекают в адсорбционном слое, играющем роль «буфера» между кристаллом и вакуумом. Адсорб­ционный слой при этом, как правило, рассматривается как двойной, т.е. содержащий анионную и катионную плоскости. Рассмотрим нес­колько подробнее процессы, лежащие в основе кинетических моделей.

При анализе адсорбции необходимо учитывать особенности, прису­щие элементам II (III) и IV (V) групп. Для описания процесса адсорб­ции вводят понятие коэффициента прилипания или адсорбции. Для металлических элементов III группы величина этого коэффициента близка к единице, и не зависит от типа атомов покрывающих поверх­ность. Другими словами, атомы III группы и некоторые атомы второй группы (Ве, Мg) могут адсорбироваться на поверхность, уже покрытую слоем атомов III (II) группы. В результате это может приводить к образованию на поверхности роста включений металлической фазы и срыву двумерного послойного роста. В случае адсорбции летучих элементов картина оказывается намного сложнее.

Во-первых, коэффициент адсорбции зависит от степени покрытия ростовой поверхности элементами V (VI) группы, причем величина его близка к нулю для поверхности стабилизированной атомами элемен­та V (VI) группы.

А во-вторых, коэффициент адсорбции зависит от химического со­става пара в падающем потоке. Величина коэффициента адсорбции, ко­торый по определению есть доля молекул падающего потока, хемисорбировавшихся на ростовой поверхности, зависит также от количества молекул, отраженных от поверхности роста. При этом в потоке молекул от подложки можно выделить две составляющих: молекулы, полностью идентичные падающим — отраженные от поверхности, и молекулы, которые термически десорбируются с поверхности. Атомы V (VI) группы имеют очень сильную зависимость коэффициента адсорбция от температуры роста. При описании миграции атомов и молекул на ростовой поверхности необходимо также учитывать зависимость подвижности атомов и молекул от температуры роста и количество атомов, составляющих молекулы.

Встраивание атомов в кристаллическую решетку и разложение кристалла, т.е. переход атомов из кристаллической решетки эпитаксиальной пленки в адсорбированный слой, — два основных процесса, происходящих между слоем адсорбированных атомов, которые мигри­руют по поверхности, и растущим кристаллом. При анализе встраи­вания атомов необходимо учитывать, что может реализовываться два принципиально различных механизма роста: двумерный и трехмерный рост. В свою очередь, при описании двумерного роста необходимо разделять рост через образование двухмерных островков и через по­степенное заполнение террас. Встраивание атомов в последнем случае происходит в углы террас, уступы и изломы. Встраивание атомов при образовании двумерных островков нового слоя имеет нуклеационную природу и характеризуется некоторой энергией активации. Реализация того или иного режима сильно зависит от условий роста и, в первую очередь, температуры подложки. Для описания процесса встраивания и разложения также вводят понятия коэффициентов встраивания и разложения.

Таким образом, при анализе кинетики необходимо решать систему двух нестационарных уравнении, которые отражают изменение поверх­ностной концентрации атомов элементов II (III) и VI (V) групп и содержат достаточно большое количество различных коэффициентов. В результате, даже при анализе закономерностей МПЭ бинарных по­лупроводников реальная картина оказывается чрезвычайно сложной.

Поэтому были предприняты попытки разработки целостного описа­ния МПЭ в рамках термодинамической модели. Тот факт, что процесс МПЭ осуществляется в неравновесных условиях, формально не дает оснований утверждать, что термодинамический подход, основываю­щийся на применении уравнений действующих масс в совокупности с уравнениями сохранения массы взаимодействующих элементов, не может описать состояния системы. Такой подход широко и с успехом применяется для описания многих химических реакций, идущих в сугубо неравновесных условиях. В случае сублимации бинарных со­единений (также сугубо неравновесного процесса) адекватность термо­динамического подхода была подтверждена многочисленными экспери­ментальными данными задолго до возникновении МПЭ [11]. Примет некие термодинамического описания к процессам роста методом МПЭ стимулирует также и возможность использования большого теоретического и экспериментального материала, накопленного в жидкофазной и газофазной эпитаксиях.

В рамках термодинамического описания МПЭ рассматривается как квазиравновесный процесс, где равновесие между газовой и твердой фазой устанавливается на поверхности растущего слоя. За равновесные параметры системы принимается температура подложки и эффектив­ные давления, соответствующие потокам молекул и атомов взаимодей­ствующих элементов от поверхности роста [12].

Для расчета составов равновесных фаз необходимо прежде всего определить число химических элементов — Э, присутствующих в рассматриваемой системе, и число компонентов — К, образуемых этими атомами. Тогда, число независимых химических реакций

r = К — Э. (3)

Независимой называется такая реакция, которая не может быть получена линейной комбинацией других. Для независимых реакций записывают уравнения закона действующих масс, включающие равновесные парциальные давления компонентов, находящихся в газовой фазе, и активности компонентов конденсированной фазы. Входящие в уравнения константы равновесия определяют по справочным термодинамическим данным.

Для расчета всех неизвестных давлений необходимо дополнить систему уравнений равновесия уравнениями материального баланса. Уравнения закона действующих масс отражают влияние температуры на равновесное состояние системы, а уравнения материального балан­са — влияние входных давлений реагентов.

При составлении уравнений материального баланса вводят поня­тие гипотетического давления элемента в газовой фазе. Равновесное гипотетическое давление связано с искомыми равновесными парци­альными давлениями компонентов уравнением

, (4)

где k_г- — число компонентов газовой фазы; v_ij —- число атомов i -го элемента в компоненте j.

Рассмотрим реакцию между основными компонентами при МПЭ

классического полупроводника — GaAs. Согласно (3), число неза­висимых реакций, описывающих МПЭ GaAs, разно r=4-2=2, принимая во внимание участие в реакции димеров двухатомных и тетрамеров четырехатомных молекул Аs:

GaAs(s) = Ga(g) + 1/2As₂(g), (5)

As₂(g) = 1/As₄(g). (6)

Согласно уравнению сохранения масс, для давлений молекулярных пучков Аs и Gа, идущих на рост, имеем

, (7)

где и давление в падающих потоках атомов мышьяка и галлия на поверхность, соответственно.

Решение системы вышеупомянутых уравнений дает значений рав­новесных парциальных давлений , и .

На рис. 7и 8 показаны рассчитанные равновесные парци­альные давления над бинарными полупроводниками InAs, GaAs, AlAs, InSb, GaSb и AlSb как функция соотношения давлений падающих по­токов элементов III и V групп и температуры подложки соответственно. При этом важно отметить, что на рис. 7 представлены результаты расчетов при различных температурах для разных полупроводников (наиболее типичных для МПЭ). Давление падающего потока элемен­тов III группы (Аl, Gа и In) принималось равным атм, а соотношение давлений потоков — равным 2.

Как видно из рис. 7, существенные изменения на графиках происходят при соотношении = 1 для всех бинарных соединений А^IIIВ^V. Другая важная особенность, очевидная из рис. 7 состоит в том, что при типичных режимах эпитаксии, когда >1, над поверхностью почти всегда преобладает пар, состоящий из двухатомных молекул элементов V группы, что полностью совпадает с экспериментальными данными [13, 14]. Давление пара четырехатом­ных элементов V группы становится соизмеримым и даже превосхо­дит давление пара двухатомных молекул, в основном, при больших соотношениях давлений и достаточно низких температурах (см. рис. 8), как, например, в случае InAs и InSb.

Из рис. 8 видно, что с увеличением температуры существен­но возрастает равновесное давление пара элементов III группы. При некоторой температуре, когда давление пара III группы сравнивается с давлением пара элементов V группы, начинается эффективное разло­жение кристалла, а эта температура хорошо согласуется с предельной температурой эпитаксии.

Скорость роста соединений А³В⁵ при условии упомянутых выше предположений может быть просто записана в виде уравнения Герца-Кнудсена:

, (8)

где _III — коэффициент встраивания атомов III группы, т — масса молекулы, k — постоянная Больцмана, V_с — объем молекулы расту­щего кристалла, Т — температура (К). При этом предполагается, что уравнения Герца-Кнудсена выполняются при температуре подложки. Поскольку _III= 1, а зависимостью Т^-1/2 в типичном температурном диапазоне эпитаксии можно пренебречь, выражение (8) можно за­писать в виде

, (9)

где k * - константа, не зависящая от температуры.

Рис 7. Зависимости равновесных давлений от соотношения давлений падавших потоков для ( атм): a) InAs, Т_п = 500С; б) InSb, Т_п = 450С; в) GaAs, Т_п = 600С; г) GaSb, Т_п = 500С; д) AlAs, Т_п = 600С; е) AlSb, Т_п = 600С.

Рис. 8. Зависимости равновесных давлений от температуры подложки

( =2; для атм) для: а) InAs; б) InSb; в) GaAs; г) GaSb;; д) AlAs; е) AlSb.

Таким образом, зависимость скорости роста от технологических параметров будет находиться из расчета величин 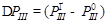. Зависимости D Р _III представлены для двух полупроводников — InAs и InSb, от давления падающего потока и соотношения давле­ний падающих потоков на рис. 9 и 10, соответственно.

Линейная зависимость D Р _III на рис. 9 от давления падающего потока In, сохраняется до тех пор, пока равновесное давление In

Рис. 9. Зависимость разности давления падающего потока и равновесного давления In 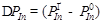от соотношения падающих потоков 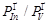для двух полупроводников: а) InAs; б) InSb.

Рис. 10.Зависимость разности давления падающего потока и равновесного давления In 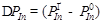от давления падающего потока In для двух полупроводников: а) InAs; б) InSb.

пренебрежимо мало в сравнении с давлением падающего потока (см. рис. 9 и 10 ). По мере уменьшения эти давления становятся соизмеримы, и при зависимость отклоняется от линейной, и величина D Р резко уменьшается. Таким образом, при типичных режимах эпитаксии скорость роста линейно зависит от входного потока элемента III группы. Поэтому при соотношении > 1 величи­на D Р _In на рис. 9постоянна и не зависят от давления падающего потока элементов V группы. При соотношении потоков < 1величина DP линейно уменьшается, т.к. скорость роста лимитируется скоростью доставки атомов Sb.

Аналогичные зависимости DP_III от входных потоков реагентов могут быть получены для всех полупроводников А^IIIВ^V и А^IIВ^VI, а твердых растворов на их основе.

При некотором фиксированном давлении сувеличением тем­пературы подложки, растет равновесное давление (см. рис. 8), и при некоторой температуре величина D Р _IIIстанет равной 0, и, соответственно, станет равна 0 и скорость роста. Зависимость скорости роста от температуры для различных полупроводников представлена на рис. 11. Скорости роста для разных полупроводников приведены

Рис. 11. Зависимость относительной скорости роста от температуры под­ложки для разных полупроводников: 1 — InSb; 2 — InAs; 3 — GaAs; 4 — Gasb; 5 — AlSb; 6 — AlAs.

к единице, при этом значение температур, до которых скорость роста не изменяется, прямо коррелирует с величиной константы равновесия. Максимальная величина константы равновесия при данной темпера­туре соответствует АlAs, минимальная — InSb. Соответственно, и температура начала резкого снижения скорости роста уменьшается от AlAs к InSb. Важно отметить, что эта температура зависит от входного потока элемента III группы и соотношения; давлений увеличением потока III группы и соотношения эта темпера­тура увеличивается.

Таким образом, в основе термодинамической модели МПЭ лежат следующие положения.

1. МПЭ рассматривается как квазиравновесный процесс, где равновесие между газовой к твердой фазой (или между газовой, жидкой и твердой фазами в случае образования сегрегационного слоя на поверхности) устанавливается на поверхности растущего слоя.

2. Основные термодинамические параметры:

• за температуру системы принимают температуру подложки;

• парциальные давления компонентов в отраженных потоках при­нимаются за равновесные;

• поток атомов от поверхности подложки рассматривается состо­ящим из двух частей: атомы входного потока, термаолизованные на поверхности и отраженные от подложки (избыточное давление на под­ложку), и потока атомов, обусловленного термической диссоциацией конденсирующегося вещества.

3. Скорость осаждения эпитаксиального слоя лимитируется скоро­стью поступления на подложку компонентов, имеющих наименьшее давление паров при температуре подложки (атомов III группы при МПЭ соединений А^IIIВ^V). В этом случае избыточный по сравнению с необходимым для связывания атомов элементов III группы поток Элементов V группы переиспаряется и лишь определяет точку на фазовой диаграмме внутри области гомогенности и, соответственно, тип и концентрацию точечных дефектов.

Термодинамический подход успешно применяется при анализе за­кономерностей роста не только бинарных полупроводников, но и более сложных соединений — твердых растворов. С использованием тер­модинамического анализа оказалось возможным объяснить влияние упругих напряжений при выращивании сильно рассогласованных по периоду кристаллической решетки полупроводников [15, 16]. В частно­сти, было показано, что возникающие вследствие дилатационного несо­ответствия напряжения приводят к переиспарению летучего компонента, поэтому начальные стадии эпитаксии в такого рода гетеропарах должны проводится при пониженной температуре роста. Более того, термодинамический подход успешно применялся и к анализу особенно­стей формирования структур с пониженной размерностью, в частности гетерограниц. В работе [17| на основании термодинамической модели нам удалось определить максимальную температуру формирования интерфейса типа InSb в структурах, не имеющих общих атомов при переходе через гетерограницу. Наконец, термодинамическая модель была успешно применена нами для описания процессов сегрегации примесей и базовых элементов на поверхности роста [18, 19, 20]. В то же время, как показали исследования, термодинамический под­ход ограниченно применим к многокомпонентным твердым растворам, содержащим несколько элементов V (VI) группы. В случае такого рода твердых растворов имеет место сильная конкуренция между атома­ми при встраивании в кристаллическую решетку, и решающую роль играют кинетические коэффициенты, т.е. необходимо использовать комбинацию термодинамического подхода с кинетическим, описанным выше.

Необходимо признать, что на сегодняшний день нет единого под­хода к описанию МПЭ. При этом термодинамический подход, который представляется наиболее обоснованным в теоретическом плане, имеет ограниченное применение, поскольку связан с минимальным количе­ством экспериментальных параметров и, как следствие, обеспечивает -минимум информации о поверхностных процессах, что не позволяет полностью описать все экспериментальные данные. В то же время, несмотря на очевидную значимость кинетических моделей для повы­шения уровня понимания процессов роста при МПЭ на микроуровне, они зачастую терпят неудачу при попытках получения количественных зависимостей.

Дата добавления: 2014-11-29