Особенности МПЭ многокомпонентных твердых растворов

Для синтеза высококачественных приборных гетероструктур, в качестве подложек используются объемные кристаллы бинарных соединений А^IIIВ^V, согласованные по периоду кристаллической решетки с осаждаемыми эпитаксиальными слоями. Согласование параметров решеток обеспечивает когерентность гетерограниц и, следователь­но, снижение интерфейсной рекомбинации, что позволяет значительно, улучшить люминесцентные и транспортные характеристики гетеро­структур.

Обеспечить согласование осаждаемого слоя с подложкой или после­дующим (предыдущим) слоем по периоду решетки можно, используя твердые растворы. Под твердым раствором понимаются соединения, образованные таким образом, что два или более элементов III (И) группы случайным образом распределены по узлам решетки, занима­емым атомами III (II) группы, или два или более элементов V (VI) группы, случайным образом распределены по узлам решетки, занимае­мым атомами V (VI) группы. Кроме согласования параметров решетки двух материалов, при выборе систем для гетероэпитаксии важную роль играет возможность варьирования ширины запрещенной зоны и зонной структуры (прямозонный полупроводник или нет).

Вследствие изоморфизма кристаллического строения твердых рас­творов период решетки а(х) твердого раствора вида A _x B_{1- x} C подчиня­ется правилу Вегарда, т.е. линейно зависит от состава х и периодов решетки входящих в него соединений:

а(х)= xa_AC + (1-x)a_BC.

Ширина запрещенной зоны квазибинарных растворов выражается, в зависимости от состава, функцией,

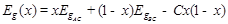, (11)

где С — параметр прогиба (нелинейности), имеющий тем большее значение, чем сильнее различие периодов решеток компонентов.

Однако трехкомпонентные растворы, характеризующиеся жестки­ми зависимостями периода решетки а(х) и ширины запрещенной зо­ны Е_g (х)от состава, не позволяют варьировать эти параметры независимо друг от друга и, таким образом, существенно ограничивают возможности использования гетероструктур в оптоэлектронике. Этого недостатка лишены четырехкомпонентные твёрдые растворы, в которых изменением состава твердого раствора можно в широких пределах изменять ширину его запрещенной зоны' при сохранении периода кри­сталлической решетки равным периоду заранее выбранной подложки Или периоду соседнего полупроводникового слоя.

Зависимость периода решетки а(х,у) от состава четырехкомпонентных твердых растворов типа A _x B_{1- x} C _yD_1-y, образованных бинарными соединениями АС, ВС, АВ и ВD, обычно описывается интерполяцион­ной формулой:

a(x, y) = xya_AC + x(1-y)a_AD + (1-x) ya_BC + (1-x)(1-y)a_BD.

Ширина запрещенной зоны Е_g (х)четырехкомпонентных твердых растворов определяется нелинейной интерполяцией:

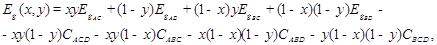(13)

где — ширины запрещенной зоны соответствующих бинарных па­лу проводников, С_ijk — параметры провисания соответствующих трех-компонентных твердых растворов (значения параметров даны в [21]).

Важно отметить, что ширина запрещенной зоны и период кри­сталлической решетки для полупроводников не является постоянным параметром, их численные значение в значительной степени зависят от температуры. Температурная зависимость ширины запрещенной зоны имеет следующий вид:

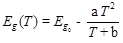, (14)

где - ширина запрещенной зоны при температуре абсолютного нуля, Т — температура, a и b — температурные коэффициенты,

Температурная зависимость периода кристаллической решетки выражается формулой

a(T) = a₀ [ 1 + a (T — T ₀)], (15)

где a ₀ — период решетки при температуре T ₀, a - коэффициент теплового расширения.

Основной проблемой при МПЭ многокомпонентных твердых раство­ров является управление составом металлоидной подрешетки. Сложности управления составом многокомпонентных твердых растворов, содержащих два летучих компонента, связаны, как уже отмечалось, с сильной конкуренцией между ними при встраивании в металлоидную подрешетку.

Наибольшее распространение получили методы контроля соста­вов (в металлоидной подрешетке) твердых растворов, основанные на определение скоростей или коэффициентов встраивания элементов VI или V группы, поскольку кинетику поверхностных процессов наибо­лее удобно описывать интегрально, через коэффициенты встраивая летучих компонентов. Впервые такой подход был предложен нами и успешно применен для количественного описания процессов МПЭ твердых растворов широкозонных соединений А^IIIВ^V: ZnSSe и MgSSe [22]. Мы использовали тот факт, что при эпитаксии ZnSSе.) оказывается возможным с большой точностью зафиксировать переход от поверхностной реконструкции (2х1)Sе к с(2х2)Zn, соответствую­щий единичному стехиометрическому соотношению потоков атомов VI и II группы на поверхность роста, поскольку ни цинк, ни элементы VI группы не могут сформировать более одного МС на поверхности роста в отсутствии друг друга. Коэффициенты встраивания Sе и S определялись из экспериментальных температурных зависимостей соотношений давлений в падающих потоках элементов VI/II групп, со­ответствующих перестройке поверхностной реконструкции от (2х1)Sе к с(2х2)Zn при росте ZnSе и ZnSSе. Для последнего определялась, также температурная зависимость состава твердого раствора, выращен­ного в с тех и о метрических условиях. Далее, определенные коэффици­енты встраивания использовались в качестве весовых коэффициентов в уравнениях материального баланса уже в рамках термодинамической модели. Данная феноменологическая модель позволила установить однозначную количественную связь между давлениями компонентов в падающих потоках, температурой подложки, с одной стороны, и скоростью роста, составом и стехиометрии растущего соединения, с другой. Данная модель получила дальнейшее развитие в [23].

В случае эпитаксии многокомпонентных твердых растворов на основе соединений А^IIIB^V картина оказывается более сложной. Как уже отмечалось, атомы элементов III группы при типичных режимах эпитаксии имеют коэффициент адсорбции, близкий к единице, что может приводить к образованию включений жидкой фазы на фронте кристаллизации. В связи с этим также существуют сложности в выявлении смены поверхностной реконструкции с V-стабилизированной к III-стабилизированной поверхности. Тем не менее, комбинированный подход, интегрально учитывающий кинетику поверхностных реакций через коэффициенты встраивая летучих компонентов, оказалось воз­можным применить и к описанию МПЭ роста твердых растворов АlGaAsSb [24]. Было обнаружено, что вопреки термодинамическому описанию при типичных температурах эпитаксии преимущественное встраивание в кристаллическую решетку имеют атомы сурьмы, при этом найденный коэффициент встраивания и двух- и четырехатомных молекул близок к единице вплоть до температур 480 °С.

В работе [25] при МПЭ для управления составом твердых растворов использовались калибровки скоростей встраивания летучих компонентов, измеряемые с помощью дифракции быстрых электронов. Суть метода состоит в том, что рост осуществляется в условиях, когда соотношение потоков III/V групп составляет ~1.2 (условия роста стабилизированные элементом III группы), при этом осцилляции Отраженного первичного пучка определяются уже не скоростью роста (поступлением атомов III группы), а скоростью поступления атомов элемента V группы [26]. Такой режим роста сопровождается резким уменьшением яркости картины ДБЭ, деградацией поверхности роста, Связанной с накоплением избыточных атомов Gа, однако в течение короткого промежутка времени (как правило, время роста несколь­ких монослоев) осцилляции ДБЭ могут быть зафиксированы. Этот метод позволяет прокалибровать скорость встраивания металлоидных компонентов. Состав твердых растворов при этом можно определить просто как арифметические соотношения скоростей встраивания. Сле­дует отметить, что такой метод успешно применяется в ряде случаев, Однако он не учитывает конкуренции между анионами при встраивании в металлоидную подрешетку при росте твердого раствора, поскольку их коэффициенты определяются для случая встраивания в бинарные полупроводники.

В работе [27] для определения коэффициента встраивания сурь­мы при эпитаксии твердых растворов (Аl, Gа) AsSb использовались масспектрометрические измерения отраженного от поверхности рос­та и падающего потоков сурьмы. Коэффициент встраива­ния сурьмы при этом определялся следующим образом:

. (16)

Такой метод наиболее точно позволяет определить коэффициен­ты встраивания металлоидов, однако его применение требует пере­оснащения установок МПЭ, поскольку необходима установка масспектрометра в блок испарительных ячеек вместо одного из источников молекулярного пучка для измерения отраженных от подложки потоков;, что сопряжено со значительными трудностями, и часто невозможно.

Сложности, связанные с управлением составом многокомпонентных твердых растворов, привели к разработке и исследованию нового клас­са объектов — твердых растворов, в которых атомы распределены по узлам решетки не случайным образом, а упорядоченно. Такой твердый раствор, по сути, является короткопериодной сверхрешеткой моноатомной толщины, причем каждая моноатомная плоскость состоит из атомов одного элемента [28]. Состав такого твердого раствора опре­деляется простым соотношением количества моноатомных плоскостей определенного сорта атомов к их общему числу. При росте такого рода твердых растворов оказывается возможным существенно умень­шить значение падающих потоков и тем самым, уменьшить фоновое давление в ростовой камере. Для синтеза «упорядоченных» твердых растворов используются модификации метода МПЭ: атомно-слоевая эпитаксия и эпитаксия с повышенной миграцией атомов [29]. Суть этих модификаций МПЭ состоит в том. что соответствующие элементы III и V групп подаются на подложку поочередно, а не одновременно.

Синтез многокомпонентных твердых растворов, необходимость ис­пользования которых продиктована требованиями обеспечения задан­ных энергетических параметров при одновременном согласовании пери­одов кристаллических решеток сопрягаемых материалов, представляет достаточно сложную технологическую задачу еще и потому, что боль­шинство многокомпонентных твердых растворов на основе полупро­водников А^IIIВ^V и А^IIВ^VI характеризуются достаточно протяженными областями несмешиваемости.

Из-за различия атомных размеров компонентов, составляющих твердый раствор, неизбежно возникают локальные искажения кристал­лической решетки твердого раствора, которые являются основной при­чиной эндотермического вклада в энтальпию смешения и отклонения поведения системы от идеального. Согласно квазихимическому при­ближению, положительность избыточной энергии смешения является проявлением тенденции к разделению пар одноименных атомов, т.е. проявлением отталкивания между атомами смешиваемых компонентов твердого раствора. Поэтому в таких системах при некоторой темпера­туре следует ожидать появления областей несмешиваемости и любой неидеальный твердый раствор при понижении температуры становится неустойчивым в определенном диапазоне составов. Твердый раствор, находящийся в области неустойчивости, стремится уменьшить свою свободную энергию в результате распада, приводящего к нарушению макроскопической однородности кристаллов и появлению смеси фаз различного состава. Распад, протекающий без образования зародышей новых фаз, называют спинодальным. При спинодальном распаде со­ставы выделяющихся фаз изменяются непрерывным образом, причем процесс фазового распада охватывает одновременно весь кристалл [30].

В соответствии с терминологией, граничную кривую на диаграмме состояний, отделяющую область составов твердых растворов, неустойчивых даже к бесконечно малым флуктуациям состава, называют спинодалью. С математической точки зрения — это геометрическое место точек, в которых имеет место смена знака кривизны кривых, выражающих зависимость свободной энергии Гиббса от состава твердого раствора.

Спинодальная изотерма разделяет нестабильную и метастабильную области составов твердых растворов. В метастабильной области одно­родный твердый раствор устойчив относительно малых отклонений от Однородного распределения атомов. Однако устойчивость может быть Потеряна при больших флуктуациях состава, которые можно рассмат­ривать как зародыши новой фазы, т.е. эволюция метастабильной сис­темы к устойчивому состоянию требует флуктуационного преодоления энергетического барьера, связанного с активационным образованием центров новой, более устойчивой фазы.

Критерий термодинамической устойчивости системы, содержащей три независимых компонента, имеет вид

. (17)

Совокупность точек, имеющих общую плоскость касания к поверх­ности энергии Гиббса, образует линию стабильных твердых фаз. Для составов, ограниченных спинодальной кривой, свободная энергия сме­си фаз имеет более низкое значение, чем свободная энергия твердого раствора.

Для математического описания бинодали необходимо приравнять химические потенциалы компонентов в сосуществующих фазах:

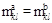. (18)

Экспериментальное изучение процессов распада и кластеризации твердых растворов весьма трудоемко и предполагает использование прецизионных методов фазового анализа. Вместе с тем, информа­ция о разрывах растворимости компонентов в твердой фазе является очень важной, поскольку несмешиваемость твердых растворов может оказаться серьезным препятствием при оптимизации технологических режимов получения эпитаксиальных слоев с заданными свойствами. Поэтому большое распространение получили теоретические модели анализа фазовой устойчивости твердых растворов: модель регулярного раствора [31] и модель «дельта параметра решетки» [32]. На резуль­таты расчетов положения областей несмешиваемости существенное влияние оказывает не только выбор модели для расчета, но и исходные термодинамические параметры. Наибольшая точность расчетов при этом может быть достигнута в рамках модели регулярного раствора при использовании для оценки параметра межатомного взаимодействия в твердой фазе стандартных термодинамических функций [33].

Важно отметить, что процесс МПЭ не подразумевает резкого изме­нения, температурных режимов, а следовательно, больших флуктуации состава, кроме того, МПЭ традиционно относят к квазиравновесным методам, что в ряде случаев позволяет синтезировать растворы с составами, попадающими внутрь химической области несмешиваемости без признаков спинодального распада [34], однако ее наличие все равно мо­жет оказывать существенное влияние на свойства твердых растворов. Кластеризация твердой фазы, в первую очередь, негативным образом отражается на оптических и транспортных свойствах гетероструктур или, например, может выражаться в виде затрудненного встраивания наиболее летучего компонента, что существенно усложняет управление составом твердых растворов. Поэтому задача точного определения положения границ областей неустойчивости в четырехкомпонентных твердых растворах не теряет актуальности и при использовании техно­логии МПЭ.

Список литературы

1. Cho A.Y., Arthur J.R. Molecular beam epitaxy//in Progress in solid state chemisty/Ed. by G. Somorjaj, J. McCaldin. Pergamon, 1975. V. 10. P. 157-190.

2. Foxon C.T. Molecular beam epitaxy//Acta Electronica. 1978. V. 21. P. 139-150.

3. Guenther K.G.//Z.Naturforsch. 1958. V. 13a. P. 1081.

4. Frank F.C., van der Merwe J.H.//Proc. Soc. London, Ser. A 198. 1949. P. 205.

5. Folmer M. Nuclei formation in supersaturated states/M. Folmer, A. Weber//Zeitschzift fur Physikalishe Chemie. 1926. V. 119. P. 227-301.

6. Stranski I.N., Krastanov L. Theory of orientation separation in Ionic Crystals//Sitzber. Acad. Wiss. Wien, Math-Natur W. 1938. V. 146. P. 797-810.

7. Matthews J.W., Blakeslee A.E.//J. of Crystal Growth. 1974. V. 27. P. 118-125.

8. People R., Bean J.C.//Appl. Phys. Lett. 1985. V. 47. P. 322-324.

9. Майссел Л., Глэнг Р. Технология тонких пленок. М.: Советское радио, 1977.

10. Foxon C.T.//Acta Electronica. 1978. V. 21. P. 139-150.

11. Крегер Ф. Химия несовершенных кристаллов. М., 1987. 651 с.

12. Копьев П.С., Леденцов Н.Н.//ФТП. 1988. Т. 22. С. 1729-1742.

13. Foxon C.T.//Acta Electronica. 1978. V. 21. P. 139-150.

14. Heckingbottom R., Davies G.J., Prior K.A.//Surf. Sci. 1983. V. 132. P. 375-389.

15. Ivanov S.V., Boudza A.A., Kutt R.N., Ledentsov N.N., Meltser B. Ya., Shaposhnikov S.V., Ruvimov S.S., Kop'ev P.S.//J. Cryst. Growth. 1995. V. 156. P. 191-205.

16. Ivanov S., Kop'ev P. Type-II (AlGa)Sb/InAs Quantum well structures and superlattices for opto- and microelectronics grown by molecular beam epitaxy. Chapter 4. In «Antimonide-related strained-layer heterostructures»/Ed. by M.O. Manasreh//Ser. «Optoelectronic properties of semiconductors and superlattices». V. 3. Gordon & Breach Science Publishers, 1997. P. 95-170.

17. Неклюдов П.В., Иванов С.В., Мельцер Б.Я., Копьев П.С.//ФТП. 1997. Т. 31. С. 1242-1245.

18. Ivanov S., Kop'ev P., Ledentsov N.N.//J. Cryst. Growth. 1990. V. 104. P. 345-354.

19. Ivanov S., Kop'ev P., Ledentsov N.N.//J. Cryst. Growth. 1991. V. 184. P. 661-669.

20. Ivanov S., Kop'ev P., Ledentsov N.N.//J. Cryst. Growth. 1991. V. 111. P. 151-161.

21. Vurgaftman I., Meyer J.R., Ram-Mohan L.R.//J. Appl. Phys. 2001. 89(11). P. 5815.

22. Ivanov S.V., Sorokin S.V., Kop'ev P.S., Kim J.R., Jung H.D., Park H.S.//J.Crystal Growth. 1996. V. 159. P. 16-20.

23. Сорокин В.С., Сорокин С.В., Кайгородов В.А. Материалы электронной техники. 2000. Вып. 4. С. 50-54.

24. Семенов А.Н., Соловьев В.А., Мельцер Б.Я., Сорокин В.С., Иванов С.В.//ФТП. 2004. Т. 38, № 3. С. 278-284.

25. Almuneau G., Hall E., Mathis S., Coldren L.A.//J. Crystal Growth. 2000. V. 208. P. 113-116.

26. Chiu T.H., Tsang W.T., Cunningham J.E., Robertson A.Jr.//J. Appl. Phys. 1987, V. 62. P. 2302-2307.

27. Evans K.R., Stutz C.E., Yu P.W., Wie C.R.//J. Vac. Sci. Technol. B. 1990. V. 8. P. 271-275.

28. Egorov A. Yu., Zhukov A.E., Kop'ev P.S., Ledentsov N.N., Maksimov M.V., Ustinov V.M.//Semiconductors. 1994. V.28. P. 363.

29. Horikoshi Y.//J. of Crystal Growth. 1999. V. 201/202. P. 150-158.

30. Кузнецов В.В., Москвин П.П., Сорокин В.С. Неравновесные явления при жидкостной гетероэпитаксии полупроводниковых твердых растворов. М.: Металлургия, 1991.

31. Jordan A.S., Ilegems M.//J. Phys. Chem. Solids. 1975. V. 36. P. 329-342.

32. Stringfellow G.B.//J. of Crystal Growth. 1974. V. 27. P. 21-34.

33. Sorokin V.S., Sorokin S.V., Semenow A.N., Meltser B.Ya., Ivanov S.V.//J. Crystal Growth. 2000. V. 216. P. 97-103.

34. Semenov A.N., Solov'ev V.A., Meltser B.Ya., Lyublinskaya O.G., Prokopova L.A., Ivanov S.V.//J. Crystal Growth. 2005. V. 278. P. 203-208.

6. КЛАССИФИКАЦИЯ ПОЛУПРОВОДНИКОВЫХ СВЕРХРЕШЕТОК

С момента появления идеи создания искусственных сверхре­шеток, высказанной Л. В. Келдышем в 1962 г. [15] и возрожденной L. Еsaki и R. Тsu в 1970 г., полупроводниковые сверхрешетки пред­ставляют собой одну из наиболее развивающихся областей физики твердого тела. Как уже отмечалось, термин «сверхрешетка» используют для периодических структур, состоящих из тонких слоев полупроводников, повторяющихся в одном направлении с периодом, меньшим длины свободного пробега электронов. В ос­новном различают два типа искусственных сверхрешеток: компо­зиционные (КСР), состоящие из периодической последовательно­сти полупроводников разного химического состава, и легированные (ЛСР), представляющие собой последовательность слоев п- и p -типа одного материала с возможными беспримесными прослойками между ними (nipi -кристаллы). Использование этих двух подходов позволило создать большое число различных сверх­решеток. Существующее разнообразие полупроводниковых СР сделало необходимой их классификацию. В данном разделе мы рассмотрим классификацию полупроводниковых сверхрешеток, в основном следуя [13].

Потенциальный профиль в КСР создается за счет периоди­ческого изменения ширины энергетической запрещенной зоны в направлении роста кристалла; в ЛСР он обусловлен электро­статическим потенциалом ионизированных примесей.

Расположение краев энергетических зон различных материалов обычно сравнивают, используя в качестве единого начала отсчета уровень вакуума. При этом каждый из рассматриваемых материа­лов характеризуют величиной электронного сродства о, которое определяет энергию, требуемую для переноса электрона со дна зо­ны проводимости материала на уровень вакуума. Поэтому в мате­риале с большим значением электронного сродства край зоны про­водимости лежит ниже по энергии, чем в материале с меньшим электронным сродством.

Использование общего начала отсчета энергии позволяет раз­делить композиционные сверхрешетки на три типа (рис. 12).

В сверхрешетках типа I разрывы зоны проводимости и валентной зоны имеют противоположные знаки, а запре­щенные зоны полностью перекрываются. Такие сверхрешетки называют также контраваршнтным композиционными сверхре­шетками.

Рис. 12. Расположение зоны проводимости и валентной зоны от­носительно уровня вакуума (штриховая линия) в отдельных неконтактирующих материалах (слева) и КСР различных типов (справа): а - СР типа 1, б - СР типа II, в - политипная СР, по оси абсцисс отложена простран­ственная координата, по оси ординат -энергия [13].

Характерной чертой данных сверхрешеток является то, что уз­козонный слой, зажатый между широкозонными слоями, образует две прямоугольные квантовые ямы - одну для электронов, а дру­гую для дырок. Глубина этих потенциальных ям зависит от того, какая часть разности ширин запрещенной зоны D E_g = E_{g 2} — E_{g 1} приходится на разрыв D E_C, а какая - на разрыв D E_V. Например, наиболее используемые в настоящее время разрывы зон гетеро­переходов GaAs - Al_xGa_1-xAs составляют 0,6D E_g для D E_С и 0,4D E_g - для D E_V.

В сверхрешетках типа II изменения краев зоны проводимо­сти и валентной зоны имеют одинаковый знак, а запрещенные зоны перекрываются лишь частично либо не перекрываются вообще (ковариантная сверхрешетка).

Характерной чертой таких сверхрешеток является пространст­венное разделение носителей, локализованных в квантовых ямах. Электроны сосредоточены в квантовых ямах, образованных одним полупроводником, а дырки - в квантовых ямах, образованных дру­гим полупроводником. Отметим, что в этих многослойных систе­мах возникает «непрямая в реальном пространстве запрещенная зона». В качестве примера на рис. 13 показаны зонные диаграммы сверхрешеток такого типа на основе систем InAs-GaSb и In_1-xGa_xAs — GaSb_1-yAs_y.

Политипная сверхрешетка (см. рис. 12, в) представляет собой трехкомпонентную систему, в которой слои, образую­щие сверхрешетки типа II, дополняются широкозонным мате­риалом, создающим потенциальные барьеры как для электронов, так и для дырок, Пример энергетических диаграмм двух типов политипных сверхрешеток представлен на рис. 14. Такие решетки конструируются из базовых многокомпонентных систем типа ВАС, АВСА, АСВСА и т.д., где А означает АlSb, В - G аSb и С - InAs.

Термином «легированные СР» принято называть периодическую последовательность слоев п - и р -типа одного и того же полупровод­ника. Результирующее распределение заряда в этом случае создает совокупность параболических потенциальных ям (рис. 15). Потен­циал объемного заряда модулирует края зон исходного материала таким образом, что электроны и дырки оказываются пространст­венно разделенными. Причем соответствующим выбором парамет­ров структуры (уровней легирования и толщин слоев) это разделе­ние можно сделать практически полным. В свою очередь пространственное разнесение минимума зоны проводимости и максимума валентной зоны кардинально сказывается на парамет­рах системы. Например, из-за малого перекрытия электронных и дырочных состояний времена электронно-дырочной рекомбинации могут на много порядков превосходить свои значения в однород­ном полупроводнике.

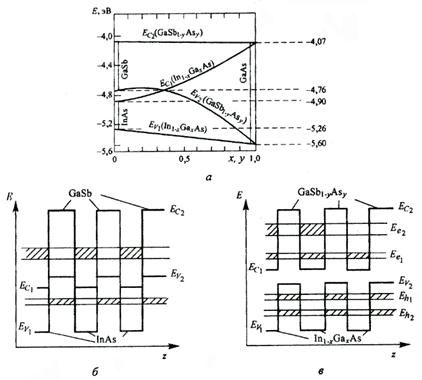
Рис 13. Зависимость положения краев зон относительно уровня вакуума в твердых растворах In_1-xGa_xAs и GaSb_1-yAs от их состава (а) и зонные диаграммы сверхрешеток InAs-GaSb (б) и In_1-xGa_xAs - GaSb_1-yAs_y, (в); заштрихованные области соответствуют энергиям подзон и участкам пространства, где концентрируются носители заряда; по оси абсцисс отложена пространственная координата [13].

Дата добавления: 2014-11-29