Распространение выборочных результатов на генеральную совокупность

Разных видов выборочного наблюдения

Вид выборки	Отбор
повторный	бесповторный
Количественный признак
Собственно-случайная
Механическая	-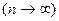
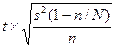
Типическая (стратифициро­ванная)
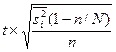
Серийная
Альтернативный признак
Собственно-случайная
Механическая	-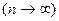
Типическая (стратифициро­ванная)
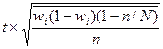
Серийная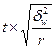

Обозначения в табл. 9.3 те же, что в табл. 9.2.

Конечной целью выборочного наблюдения является характеристика генеральной совокупности. При малых объемах выборки эмпирические оценки параметров (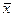 и w) могут существенно отклоняться от их истинных значений ( 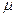и р). Поэтому возникает необходимость установить границы, в пределах которых для выборочных значений параметров ( 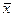и w) лежат истинные значения ( 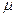и р).

Доверительным интервалом какого-либо параметра генеральной совокупности называется случайная область значений этого параметра, которая с вероятностью, близкой к 1 (надежностью) содержит истинное значение этого параметра.

Предельная ошибка выборки 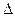позволяет определить предельные значения характеристик генеральной совокупности и их доверительные интервалы, которые равны

для средней , (4а)

для доли . (4б)

Нижняя граница доверительного интервала получена путем вычитания предельной ошибки из выборочного среднего (доли), а верхняя - путем ее добавления.

Доверительный интервал для средней использует предельную ошибку выборки и для заданного уровня достоверности p определяется по формуле

, (5а)

а для относительного параметра (доли)

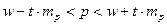. (5б)

Это означает, что с заданной вероятностью P, которая называется доверительным уровнем и однозначно определяется значением t, можно утверждать, что истинное значение средней лежит в пределах от до , a истинное значение доли w - в пределах от до .

При расчете доверительного интервала для трех стандартных доверительных уровней Р = 95%, Р = 99% и Р = 99,9% значение t вы­бирается по таблице критических точек распределения Стьюдента, в зависимости от числа степеней свободы v = п - 1. Если объем выборки достаточно велик, то соответствующие этим вероятностям значения t равны: 1,96, 2,58 и 3,29. Таким образом, предельная ошибка выборки позволяет определить предельные значения характеристик генеральной совокупности и их доверительные интервалы.

Распространение результатов выборочного наблюдения на генеральную совокупность в социально-экономических исследованиях имеет свои особенности, так как требует полноты представительности всех ее типов и групп. Основой для возможности такого распространения является расчет относительной ошибки

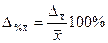- для средней;

- для доли.

Существуют два основных метода распространения выборочного наблюдения на генеральную совокупность: прямой пересчет и способ коэффициентов.

Сущность прямого пересчета заключается в умножении выборочного среднего значения 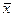на объем генеральной совокупности N.

Пример. Пусть среднее число детей ясельного возраста в городе оценено выборочным методом и составило 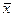= 1,2 человека. Если в городе 1000 молодых семей, то число необходимых мест в муници­пальных детских яслях получают умножением этой средней на чис­ленность генеральной совокупности N = 1000, т. е. составит 1200 мест.

Способ коэффициентов целесообразно использовать в случае, когда выборочное наблюдение проводится с целью уточнения данных сплошного наблюдения.

При этом используют формулу

, (6)

где все переменные - это численность совокупности:

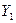- с поправкой на недоучет;

- без этой поправки;

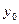- в контрольных точках;

- в тех же точках по данным контрольных мероприятий.

Дата добавления: 2014-11-29