
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Распределение наблюдений по срокам появления
|
|
|
|
Пример 3. Вычисление среднего значения и доверительного овала для дискретного признака, заданного интервальным рядом.
В табл. 9.5 задано распределение заявок на изготовление заказов по срокам их выполнения предприятием.
Таблица 9.5
| Срок выполнения заявок, мес. | Число наблюдений, 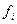 (абсолютная частота) (абсолютная частота)
| Относительная частота, 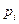 , % , %
| Середина интервала (градации) признака, 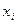
|
| До 6 | |||
| 6 - 12 | |||
| 12 - 36 | |||
| 36 - 60 | |||
| Свыше 60 | |||
| Всего |
Решение. Средний срок выполнения заявок вычисляется по формуле
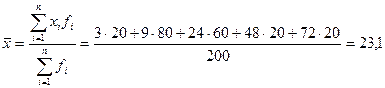 мес.
мес.
Тот же ответ получим, если используем данные об относительной частоте 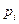 из предпоследней колонки табл. 9.5, используя формулу
из предпоследней колонки табл. 9.5, используя формулу
 мес.
мес.
Заметим, что середина интервала для последней градации находится путем искусственного ее дополнения шириной интервала предыдущей градации, равной 60 - 36 = 24 мес.
Дисперсия вычисляется по формуле:
 ,
,
а средняя квадратическая погрешность s = 30.
Средняя ошибка выборочной средней равна:
 мес.,
мес.,
т. е. среднее значение равно х ± т = 23,1 ± 13,4.
Предельную ошибку вычислим по формуле из табл. 9.3 повторного отбора, так как численность генеральной совокупности N неизвестна и для уровня достоверности P = 0,954
 дней.
дней.
Таким образом, среднее значение равно  , т.е. его истинное значение лежит в пределах от 0 до 50 мес.
, т.е. его истинное значение лежит в пределах от 0 до 50 мес.
Пример 4. Для определения скорости расчетов с кредиторами в коммерческом банке необходимо провести выборочное обследование методом случайного бесповторного отбора  предприятий корпорации. Определить необходимый объем выборки п, чтобы с вероятностью Р = 0,954 ошибка среднего значения выборки не превышала 3-х дней, если пробные оценки показали, что среднее квадратическое отклонение s составило 10 дней.
предприятий корпорации. Определить необходимый объем выборки п, чтобы с вероятностью Р = 0,954 ошибка среднего значения выборки не превышала 3-х дней, если пробные оценки показали, что среднее квадратическое отклонение s составило 10 дней.
Решение. Для определения числа необходимых исследований п воспользуемся формулой для бесповторного отбора из табл. 9.4
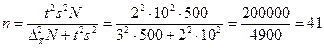 ,
,
т. е. выборку достаточно составить из 41 предприятия, чтобы оценить требуемый параметр - скорость расчетов с кредиторами.
В использованной формуле значение t определяется из таблицы Стьюдента (приложение 2) для уровня достоверности Р = 0,954. Оно равно 2. Среднее квадратическое отклонение s = 10, объем генеральной совокупности N = 500, а предельная ошибка среднего значения 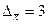 .
.
Контрольные вопросы
(выберите правильный ответ)
1. Выборка какого объема считается "малой" для одномерной случайной величины?
а) менее 5;
б) менее 10;
в) менее 30;
г) менее 100.
2. Для сопоставления эффективности работы двух поликлиник города организовано наблюдение, оценивающее количество обращений к терапевту и время обслуживания пациентов. Для этого 10% пациентов случайно отобраны из всех прикрепленных к поликлинике по букве алфавита, с которой начинается фамилия. Какой способ организации выборки использован в исследовании?
а) собственно-случайный;
б) механический;
в) стратифицированный;
г) серийный;
д) комбинированный.
3. Для задачи в тестовом примере 2 определить, какими формулами необходимо воспользоваться для оценки частоты обращений к врачу:
а)  ; б)
; б) 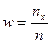 ; в)
; в) 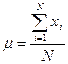 ; г)
; г) 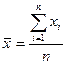 ; д)
; д) 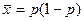 .
.
4. Социальными службами оценивается разница в частоте выдачи Сбербанком кредита на строительство для мужчин и женщин в зависимости от совокупного дохода их семей. Определить: а) тип анализируемого признака; б) какие статистики возможно для него вычислить.
а) 1) атрибутивный; 2) количественный; 3) дискретный; 4) альтернативный;
б) формулы из табл. 9.1 с номерами: 1) 2,1; 2) 2,5; 3) 2,6; 4) 2,7; 5)2,8.
5. В задаче тестового примера 4 определить формулу, по которой следует исчислить дисперсию размера кредита, выданного банком, при выборочном наблюдении:
а) 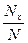 ; б)
; б)  ; в)
; в)  ; г)
; г)  .
.
6. Как оценить среднюю ошибку при вычислении среднего размера депозита граждан, содержащих в банке свои сбережения (при повторном выборочном наблюдении)?
а)  ; б)
; б) 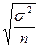 ; в)
; в) 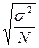 ; г)
; г)  .
.
7. Чему равно критическое значение показателя Стьюдента, если объем выборки наблюдений при оценке числа ошибок оператора ЭВМ составил 6, а допустимый уровень ошибочного заключения задан равным 5%?
а) 3,0; б) 2,57; в) 4,3; г) 6,86.
8. Чему равна предельная ошибка выборки при повторном отборе, если гарантируемая вероятность равна Р = 0,683, объем выборки п = 100, а  = 1?
= 1?
а) 0,1; б) 0,01; в) 10,0; г) 1,0; д) 0,5.
9. По какой формуле следует определять предельную ошибку выборки при оценке среднего значения при случайном бесповторном способе формирования выборочной совокупности?
а) 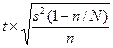 ; б)
; б)  ; в)
; в)  ; г)
; г) 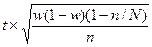 .
.
10. Чему равен требуемый объем выборки, если предельная ошибка эксперимента составляет 0,1; дисперсия равна 1, а значение критерия Стьюдента равно 2?
а) 10; б) 200; в) 400; г) 50; д) 1000.
|
|
|
|
|
Дата добавления: 2014-11-29; Просмотров: 586; Нарушение авторских прав?; Мы поможем в написании вашей работы!