Средние индексы

Средние индексы применяются в том случае, когда в исходной информации нет данных для расчета индексов в агрегатной форме. Получают средний индекс путем замены в исходном агрегатном ин­дексе индексируемого показателя его выражением, выведенным из индивидуального индекса. Если такая замена произведена в числите­ле исходного агрегатного индекса, то получим средний арифметиче­ский индекс, а если в знаменателе, то - средний гармонический ин­декс. Рассмотрим методику такого преобразования на примере индек­сов физического объема товарооборота и цен.

Например, имеются следующие данные фирмы о продаже фруктов (табл. 10.2).

Таблица l0.2.

	Товарооборот базисно­го периода, тыс. руб.	Индексы физического объема товарооборота
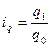
Яблоки		1,15
Апельсины		1,06
Итого		-

Знаменатель этого индекса - товарооборот базисного периода, известен, а данных для расчета числителя нет, но есть индивидуаль­ные индексы физического объема товарооборота, исчисляемые по формуле , откуда . Подставив это выражение в числитель агрегатного индекса, получим средний арифметический ин­декс физического объема товарооборота

.

Рассчитаем его:

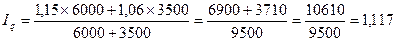, или 111,7%.

На практике средние арифметические индексы используются при расчете индексов объемных показателей, когда знаменатель ис­ходного агрегатного индекса является реальной величиной. Весами индивидуальных индексов в них являются слагаемые знаменателя исходного агрегатного индекса.

Теперь допустим, что по той же фирме известны следующие данные (табл. 10.3).

	Товарооборот отчет­ного периода, тыс. руб.	Индексы цен
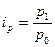
Яблоки		1,08
Апельсины		0,93
Итого		-

Агрегатный индекс цен определяется по формуле

.

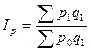Числитель этого индекса - реальный товарооборот отчетного периода - известен, а данных для расчета знаменателя нет, но извест­ны индивидуальные индексы цен, исчисленные по формуле 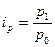, откуда 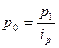. Подставив это выражение в знаменатель формулы агрегатного индекса цен, получим средний гармонический индекс цен

.

Рассчитаем его величину для примера:

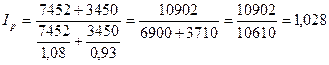, или 102,8%.

На практике средние гармонические индексы используются при расчете индексов качественных показателей, когда числитель агрегатного индекса является реальной величиной. Весами индивидуаль­ных индексов в них являются слагаемые числителя исходного агрегатного индекса.

Дата добавления: 2014-11-29