Виды рядов динамики. Методы расчета среднего уровня в рядах динамики

Тема 11. Ряды динамики

Ряды динамики - это ряды статистических показателей, ха­рактеризующих развитие явлений природы и общества во времени. Публикуемые Госкомстатом России статистические сборники содер­жат большое количество рядов динамики в табличной форме. Ряды динамики позволяют выявить закономерности развития изучаемых явлений.

Ряды динамики содержат два вида показателей. Показатели времени (годы, кварталы, месяцы и др.) или моменты времени (на начало года, на начало каждого месяца и т.п.), и показатели уровней ряда. Показатели уровней рядов динамики могут быть выражены аб­солютными величинами (производство продукта в тоннах или руб­лях), относительными величинами (удельный вес городского населе­ния в процентах) и средними величинами (средняя заработная плата работников отрасли по годам и т. п.). В табличной форме ряд дина­мики содержит два столбца или две строки.

Правильное построение рядов динамики предполагает выпол­нение ряда требований:

1) все показатели ряда динамики должны быть научно обосно­ванными, достоверными;

2) показатели ряда динамики должны быть сопоставимы по времени, т. е. должны быть исчислены за одинаковые периоды вре­мени или на одинаковые даты;

3) показатели ряда динамики должны быть сопоставимы по территории;

4) показатели ряда динамики должны быть сопоставимы по со­держанию, т. е. исчислены по единой методологии, одинаковым спо­собом;

5) показатели ряда динамики должны быть сопоставимы по кругу учитываемых хозяйств. Все показатели ряда динамики должны быть приведены в одних и тех же единицах измерения.

Статистические показатели могут характеризовать либо результаты изучаемого процесса за период времени, либо состояние изу­чаемого явления на определенный момент времени, т. е. показатели могут быть интервальными (периодическими) и моментными. Соответственно первоначально ряды динамики могут быть либо интервальными, либо моментными. Моментные ряды динамики в свою очередь могут быть с равными и неравными промежутками времени.

Первоначальные ряды динамики могут быть преобразованы в ряд средних величин и ряд относительных величин (цепной и базис­ный). Такие ряды динамики называют производными рядами дина­мики.

Методика расчета среднего уровня в радах динамики различна, обусловлена видом ряда динамики. На примерах рассмотрим виды рядов динамики и формулы для расчета среднего уровня.

Интервальные ряды динамики. Уровни интервального ряда ха­рактеризуют результат изучаемого процесса за период времени: про­изводство или реализация продукции (за год, квартал, месяц и др. пе­риоды), число принятых на работу, число родившихся и т. п. Уровни интервального ряда можно суммировать. При этом получаем такой же показатель за более длительные интервалы времени.

Средний уровень в интервальных рядах динамики исчисля­ется по формуле средней арифметической простой

,

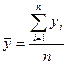где 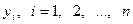- уровни ряда,

п - число периодов (число уровней ряда).

Рассмотрим методику расчета среднего уровня интервального ряда динамики на примере данных о продаже сахара в России (табл. 11.1).

Таблица 11.1

Годы	Продано сахара, тыс. г.

, тыс. т,

т. е. это среднегодовой объем реализации сахара населению России за 1994 -1996 гг. Всего за три года было продано 8137 тыс. т сахара.

Моментные ряды динамики. Уровни моментных рядов динамики характеризуют состояние изучаемого явления на определенные моменты времени. Каждый последующий уровень включает в себя полностью или частично предыдущий показатель. Так, например, число работников на 1 апреля 1999 г. полностью или частично вклю­чает число работников на 1 марта.

Если сложить эти показатели, то получим повторный счет тех работников, которые работали в течение всего месяца. Полученная сумма экономического содержания не имеет, это расчетный показа­тель.

В моментных рядах динамики с равными интервалами време­ни средний уровень ряда исчисляется по формуле средней хронологи­ческой

,

где 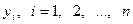- уровни моментного ряда;

п - число моментов (уровней ряда);

п - 1 - число периодов времени (лет, кварталов, месяцев).

Рассмотрим методику такого расчета по следующим данным о списочной численности работников предприятия за 1 квартал.

Таблица 11.2

Момент времени	Число работников
На 1 января
На 1 февраля
На 1 марта
На 1 апреля

Необходимо вычислить средний уровень ряда динамики, в данном примере - среднюю списочную численность работников предприятия:

человек.

Расчет выполнен по формуле средней хронологической. Сред­няя списочная численность работников предприятия за 1 квартал со­ставила 155 человек. В знаменателе - 3 месяца в квартале, а в числи­теле (465) - это расчетное число, экономического содержания не имеет. В подавляющем числе экономических расчетов месяцы, независи­мо от числа календарных дней, считаются равными.

В моментных рядах динамики с неравными интервалами времени средний уровень ряда исчисляется по формуле средней арифметической взвешенной. В качестве весов средней величины принимается про­должительность времени (t -дни, месяцы). Выполним расчет по этой формуле.

Списочная численность работников предприятия за октябрь такова: на 1 октября - 200 человек, 7 октября принято 15 человек, 12 октября уволен 1 человек, 21 октября принято 10 человек и до конца месяца приема и увольнения работников не было. Эту инфор­мацию можно представить в следующем виде (табл. 11.3).

Таблица 11.3

Число работников	Число дней (период времени)
	6 (с 1 по 6 включительно)
	5 (с 7 по 11 включительно)
	9 (с 12 по 20 включительно)
	11 (с 21 по 31 включительно)

При определении среднего уровня ряда надо учесть продол­жительность периодов между датами, т. е. применять формулу сред­ней арифметической взвешенной:

человек.

В данной формуле числитель 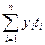имеет экономическое со­держание. В приведенном примере числитель (6665 человеко-дней) - это календарный фонд времени работников предприятия за октябрь. В знаменателе (31 день) - календарное число дней в месяце.

В тех случаях, когда имеем моментный ряд динамики с нерав­ными интервалами времени, а конкретные даты изменения показателя неизвестны исследователю, то сначала надо вычислить среднюю ве­личину для каждого интервала времени по формуле средней арифметической простой, а затем вычислить средний уровень для всего ряда динамики, взвесив исчисленные средние величины про­должительностью соответствующего интервала времени 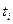. Форму­лы имеют следующий вид:

.

Рассмотренные выше ряды динамики состоят из абсолютных показателей, получаемых в результате статистических наблюдений. Построенные первоначально ряды динамики абсолютных показате­лей могут быть преобразованы в ряды производные: ряды средних величин и ряды относительных величин. Ряды относительных вели­чин могут быть цепные (в % к предыдущему периоду) или базисные (в % к начальному периоду, принятому за базу сравнения). Рас­чет среднего уровня в производных рядах динамики выполняется по другим формулам.

Ряд средних величин. Сначала преобразуем приведенный выше моментный ряд динамики с равными интервалами времени в ряд средних величин. Для этого вычислим среднюю списочную числен­ность работников предприятия за каждый месяц, как среднюю из по­казателей на начало и конец месяца :

за январь 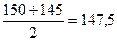; за февраль ; за март: .

Представим это в табличной форме.

Таблица 11.4

Месяцы	Среднесписочная численность работников
Январь	147,5
Февраль	153,5
Март	164,0

Средний уровень в производных рядах средних величин рас­считывается по формуле средней арифметической простой:

человек.

Заметим, что средняя списочная численность работников предприятия за 1 квартал, вычисленная по формуле средней хроноло­гической на базе данных на 1 число каждого месяца, и вычисленная по формуле средней арифметической по данным производного ряда, равны между со­бой, т. е. 155 человек. Сравнение расчетов позволяет понять, почему в формуле средней хронологической начальный и конечный уровни ряда берутся в половинном размере, а все промежуточные уровни берутся в полном размере.

Ряды средних величин, производные от моментных или интервальных рядов динамики, не следует смешивать с рядами динамики, g которых уровни выражены средней величиной. Например, средняя урожайность пшеницы по годам, средняя заработная плата и т. д.

Ряды относительных величин. В экономической практике очень широко используют ряды относительных величин. Практиче­ски любой первоначальный ряд динамики можно преобразовать в ряд относительных величин. По сути, преобразование означает замену абсолютных показателей ряда относительными величинами динами­ки.

Средний уровень ряда в относительных рядах динамики назы­вается среднегодовым темпом роста. Методы его расчета и анализа рассмотрены ниже.

Дата добавления: 2014-11-29