Анализ рядов динамики

Для обоснованной оценки развития явлений во времени необ­ходимо исчислить аналитические показатели: абсолютный прирост, коэффициент роста, темп роста, темп прироста, абсолютное значение одного процента прироста.

В табл. 11.3 приведен цифровой пример, а ниже даны формулы расчета и экономическая интерпретация показателей.

Таблица 11.5

Анализ динамики производства продукта "А " по предприятию за 1994 -1998 гг.

Годы	Произведено, тыс. т	Абсолют­ные приросты, тыс. т	Коэффи­циенты роста	Темпы роста, %	Темпы при­роста, %	Значе­ние 1% при­роста, тыс. т
цеп­ные	базисные	цеп­ные	базисные	цеп­ные	базисные	цеп­ные	базисные
		-	-	-	1,00	-		-	-	-
				1,050	1,05	105,0		5,0	5,0	2,00
				1,038	1,09	103,8		3,8	9,0	2,10
				1,055	1,15	105,5		5,5	15,0	2,18
				1,017	1,17	101,7		1,7	17,0	2.30

Абсолютные приросты 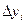показывают, на сколько единиц изменился последующий уровень ряда по сравнению с предыдущим (гр. 3 - цепные абсолютные приросты) или по сравнению с началь­ным уровнем (гр. 4 - базисные абсолютные приросты). Формулы расчета можно записать следующим образом:

;

где - базисный абсолютный прирост;

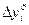- цепной абсолютный прирост;

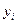- уровень ряда за отчетный период;

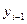- уровень ряда предыдущего периода;

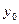- начальный уровень ряда.

Показатели абсолютного прироста свидетельствуют о том, что, например, в 1998 г. производство продукта " А " увеличилось по сравнению с 1997 г. на 4 тыс. т, а по сравнению с 1994 г. - на 34 тыс. т; по остальным годам см. табл. 11.5 гр. 3 и 4.

Коэффициент роста показывает, во сколько раз изменился уровень ряда по сравнению с предыдущим (гр.5 - цепные коэффици­енты роста или снижения) или по сравнению с начальным уровнем (гр.6 - базисные коэффициенты роста или снижения). Формулы рас­чета можно записать следующим образом:

.

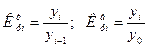Темпы роста показывают, сколько процентов составляет по­следующий уровень ряда по сравнению с предыдущим (гр. 7 - цеп­ные темпы роста) или по сравнению с начальным уровнем (гр. 8 -базисные темпы роста). Формулы расчета можно записать следую­щим образом:

, или .

Так, например, в 1997 г. объем производства продукта " А " по сравнению с 1996 г. составил:

,

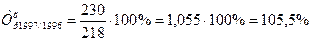а по сравнению с 1994 г.

.

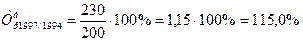Темпы прироста показывают, на сколько процентов увеличился уровень отчетного периода по сравнению с предыдущим (гр. 9 - цепные темпы прироста) или по сравнению с начальным уровнем (гр. 10 - базисные темпы прироста). Формулы расчета можно записать еле-дующим образом:

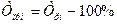или .

Так, например, в 1996 г. по сравнению с 1995 г. продукта " А " произведено больше на 3,8 % (103,8%- 100%) или 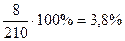, а по сравнению с 1994 г. - на 9% (109% - 100%).

Если абсолютные уровни в ряду уменьшаются, то темп будет меньше 100% и соответственно будет темп снижения (темп прироста со знаком минус).

Абсолютное значение 1% прироста (гр. 11) показывает, на сколь­ко единиц надо произвести больше в данном периоде, чтобы уровень данного периода возрос по сравнению с предыдущим на 1 %. В нашем примере в 1995 г. надо было произвести 2,0 тыс. т, а в 1998 г. - 2,3 тыс. т, т. е. значительно боль­ше.

Определить величину абсолютного значения 1% прироста можно двумя способами:

1) уровень предшествующего периода разделить на 100;

2) цепные абсолютные приросты разделить на соответствую­щие цепные темпы прироста.

Абсолютное значение 1 % прироста равно:

.

В динамике, особенно за длительный период, важен совмест­ный анализ темпов прироста с содержанием каждого процента при­роста или снижения.

Рассмотренная методика анализа рядов динами­ки применима как для рядов динамики, уровни которых выражены абсолютными величинами (т, тыс. руб., число работников и т. д.), так и для рядов динамики, уровни которых выражены относительными показателями (процент брака, процент зольности угля и др.), или средними величинами (средняя урожайность в ц/га, средняя заработ­ная плата и т. п.).

Наряду с рассмотренными аналитическими показателями, ис­числяемыми за каждый год в сравнении с предшествующим или на­чальным уровнем, при анализе рядов динамики необходимо исчис­лить средние за период аналитические показатели: средний уровень ряда, средний годовой абсолютный прирост (уменьшение) и средний годовой темп роста и темп прироста.

Методы расчета среднего уровня ряда динамики были рассмот­рены выше. В рассматриваемом нами интервальном ряду динамики средний уровень ряда исчисляется по формуле средней арифметиче­ской простой

тыс. т.

Среднегодовой объем производства продукта за 1994 - 1998 гг. составил 218,4 тыс. т.

Среднегодовой абсолютный прирост исчисляется также по формуле средней арифметической простой

тыс. т.

Ежегодные абсолютные приросты изменялись по годам от 4 до 12 тыс.т (см. гр. 3), а среднегодовой прирост производства за период 1995 - 1998 гг. составил 8,5 тыс. т.

Методы расчета среднего темпа роста и среднего темпа прирос­та требуют более подробного рассмотрения. Рассмотрим их на при­мере приведенных в таблице годовых показателей уровня ряда.

Средний годовой темп роста и средний годовой темп прирос­та. Прежде всего, отметим, что приведенные в табл. 11.5 темпы роста (гр. 7 и 8) являются рядами динамики относительных величин - про­изводными от интервального ряда динамики (гр. 2). Ежегодные тем­пы роста (гр. 7) изменяются по годам (105%; 103,8%; 105,5%;. 101,7%). Как вычислить среднюю величину из ежегодных темпов роста? Эта величина называется среднегодовым темпом роста.

Среднегодовой темп роста исчисляется в следующей последо­вательности:

1) по формуле средней геометрической исчисляют среднегодо­вой коэффициент роста (снижения) ;

2) на базе среднегодового коэффициента роста определяют среднего­довой темп роста путем умножения коэффициента роста на 100%:

.

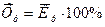Среднегодовой темп прироста определяют путем вычита­ния из темпа роста 100%:

.

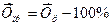Среднегодовой коэффициент роста (снижения) по формулам средней геометрической может быть исчислен двумя способами:

1) на базе абсолютных показателей ряда динамики по формуле:

,

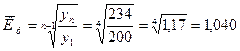где: п - число уровней;

п - 1 - число лет в период;

2) на базе ежегодных коэффициентов роста по формуле:

,

где: т - число коэффициентов.

Результаты расчета по формулам равны, так как в обеих фор­мулах показатель степени - число лет в периоде, в течение которого происходило изменение. А подкоренное выражение - это коэффици­ент роста показателя за весь период времени (см. табл. 11.5, гр. 6, по строке за 1998 г.).

Среднегодовой темп роста равен

.

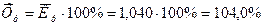Среднегодовой темп прироста определяется путем вычитания из среднегодового темпа роста 100%. В нашем примере среднегодо­вой темп прироста равен:

.

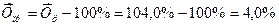Следовательно, за период 1995 - 1998 гг. объем производства продукта " А " в среднем за год возрастал на 4,0%. Ежегодные темпы прироста колебались от 1,7% в 1998 г. до 5,5% в 1997 г. (за каждый год темпы прироста см. в табл. 11.5, гр. 9).

Среднегодовой темп роста (прироста) позволяет сравнивать динамику развития взаимосвязанных явлений за длительный период времени (например, среднегодовые темпы роста численности рабо­тающих по отраслям экономики, объема производства продукции и др.), сравнивать динамику какого-либо явления по разным странам, исследовать динамику какого-либо явления по периодам историче­ского развития страны.

Дата добавления: 2014-11-29