Вторая форма уравнений Лагранжа

Exp. Res., 1077

Отметим, что именно отсюда берет начало термин самоиндукция, т. е. индукция в своем собственном магнитном поле. Переводчик.

Faraday. Exp. Res., 283.

Exp. Res. 1618.

Обоснование положения, что электрический ток есть явление кинетического характера, позволило Максвеллу дать стройное математическое исследование этого явления с помощью второй формы уравнений Лагранжа.

Прежде чем перейти к краткому изложению сущности того метода исследования динамических явлений, математическим выраже­нием которого является вторая форма лагранжевых уравнений, приведем еще несколько первых параграфов из V главы II тома максвеллова трактата, посвященной уравнениям движения связан­ных систем. Эти параграфы чрезвычайно интересны как попытка Максвелла дать физическое толкование тем обобщениям, которые были сделаны Лагранжем.

553. „В четвертом разделе второй части „Аналитической механики" Лагранж дал метод, позволяющий уменьшить число уравнений динамики, определяющих движение частей связанной системы, до числа степеней свободы системы".

„Уравнения движения связанной системы были даны Гамильто­ном в другой форме и привели к значительному развитию высшей части чистой динамики".

„Так как в дальнейшем, в связи с нашим стремлением перенести исследование электрических явлений в область динамики, нам будет необходимо уметь выразить наши динамические представле­ния в форме, пригодной для непосредственного приложения к вопросам физики, то мы посвятим настоящую главу изложению этих идей динамики с физической точки зрения".

554. „Целью Лагранжа было подчинить динамику методам высшего анализа. Он начал с представления элементарных со-

отношений динамики в виде соответствующих соотношений между чисто алгебраическими количествами и из полученных таким обра­зом уравнений вывел чисто алгебраически же свои окончательные уравнения. Некоторые количества (выражающие реакции между частями системы, вызванные ее физическими связями) входят в уравнения движения отдельных частей системы, и исследование Лагранжа является, с математической точки зрения, методом исключения этих количеств из окончательных уравнений".

„В процессе этого исключения мы имеем дело с чистым анали­зом и должны поэтому быть свободны от оперирования с идеями динамики. В противоположность этому, наша цель состоит в укрепле­нии наших динамических представлений. Мы, таким образом, пользуемся трудами математиков и переводим их результаты с языка математики на язык динамики так, чтобы наше изложение вызвало представление не об алгебраическом процессе, а б не­которых свойствах движущихся тел".

„Язык динамики значительно обогащен теми, кто развивал в общедоступной форме принцип сохранения энергии, и мы увидим, что многие из нижеследующих положений являются результатом исследования, изложенного в Natural Philosophy Томсона и Тэта, в особенности метод, исходящий из теории импульсивных сил".

„Я применил этот метод таким образом, чтобы исключить не­посредственное рассмотрение движения отдельных частей системы, кроме координат или независимых переменных, от которых зависит движение системы в целом. Важно, конечно, чтобы изучающий умел проследить связь движения каждой части системы с измене­нием (независимых) переменных, но нет надобности делать это в процессе вывода окончательных уравнений, которые не зависят от частной формы связей".

„Переменные".

555. „Число степеней свободы системы равно числу данных, необходимых для полного определения ее положения. Эти данные могут быть весьма различны по своей форме, но число их "зависит от природы самой системы и не может быть изменено".

„Чтобы уяснить нашу мысль, мы можем представить себе си­стему связанной посредством подходящего механизма с некоторым числом ползунов, каждый из которых может двигаться вдоль прямой линии и не способен двигаться как-либо иначе. Воображаемый механизм, который соединяет каждый из этих ползунов с системой, мы должны мыслить свободным от трения и инерции и неспособ­ным деформироваться под действием приложенных сил. Употребле­ние этого механизма должно лишь помочь нашему воображению в приписывании положения, скорости и количества движения тем величинам, которые фигурируют в исследовании Лагранжа как чисто алгебраические количества".

„Пусть q обозначает положение одного из ползунов, опре­деляемое как его расстояние от некоторой неподвижной точки на линии его движения. Мы будем различать величины q, соответствую-

щие различным ползунам, с помощью индексов 1, 2 и т. д. Если мы имеем дело с группой величин, относящихся к одному ползуну, мы можем опустить индекс".

„Когда величины всех (независимых) переменных (q) даны, положение каждого ползуна известно, и тем самым, с помощью воображаемого механизма, определяется конфигурация всей системы".

„Скорости",

556. „При движении системы ее конфигурация определенным образом меняется, и так как конфигурация в каждый данный момент полностью определяется величинами (независимых) пере­менных (q), то скорость каждой части системы, равно как и ее конфигурация, будут вполне определены, если нам известны

величины (независимых) переменных и их скоростей (dq/dt или, употребляя обозначения Ньютона, q) ".

„Силы".

557. „Соответственным регулированием движения ползунов, т. е. надлежащим изменением переменных, можно получить любое движе­ние системы, совместимое с природой ее связей. Чтобы произвести это движение перемещением ползунов, к последним должны быть приложены силы".

„Мы будем обозначать силу, которая должна быть приложена к переменной q_r, через F_r. Система сил (F) механически эквивалентна (в силу связей системы) той системе сил, какова бы она ни была, которая на самом деле производит движение".

Ограничиваемся этими цитатами из Максвелла, в достаточной мере характеризующими его стремление дать возможно более доступное толкование лагранжевым обобщенным координатам и обобщенным силам. Приведенные слова Максвелла мы будем рассматривать как общее введение к настоящему параграфу и теперь обратимся к ознакомлению с интересующим нас методом Лагранжа.

Итак, если электрический ток имеет кинетическую природу, то для его изучения возможно применить уравнения динамики.

Как известно из механики, движение системы в обычных случаях, при отсутствии сопротивлений, поглощающих кинетическую энергию, принято определять дифференциальными уравнениями:

где m ₁, m ₂....... m _s— массы отдельных точек системы;

x ₁, y ₁, z ₁, x ₂........ z_s — координаты точек системы; X ₁, Y ₁, z ₁, Х₂..... Z_s— проекции на координатные оси сил, приложенных к отдельным точкам системы; l ₁, l ₂....... l _k — коэффициенты связей.

Кроме того, в уравнения входит ряд функций:

f ₁(x ₁, y ₁, z ₁, х₂,.......... x_s, y_s, z_s)= 0

f ₂ (x ₁, y ₁, x ₁, x ₂ ,......... x_s, y_s, z_s)= 0

………………………………………

f _k(x ₁, y ₁, z ₁, x ₂,............ x _s, y _s, z _s)=0,

которые представляют собою выражения k кинематических связей, которым могут быть подчинены декартовы координаты системы.

Однако, эта так называемая первая форма уравнений Лагранжа не может быть применена для изучения системы электрических токов, так как, во-первых, мы не умеем описывать электрокинети­ческий процесс, пользуясь декартовыми координатами и понятием об обычной массе, а во-вторых, нам неизвестен характер связей, существующих в системе. Поэтому для анализа кинетического про­цесса, совершающегося в системе токов (такую систему иногда называют электродинамической), Максвелл воспользовался так называемой второй формой уравнений Лагранжа.

Преимущества этих уравнений (второй формы) заключаются в следующем. Во-первых, предоставляется широкая свобода в выборе координат, которые не должны быть обязательно геометрическими координатами, но могут быть любыми физическими величинами, определяющими состояние системы; во-вторых, в этом случае не требуется знания характера связей; наконец, вторая форма лагранжевых уравнений содержит только независимые переменные, силы и кинетическую энергию системы. Именно, эти уравнения имеют вид:

Отсюда непосредственно получаются выражения для внешних сил, действующих в системе и изменяющих ее кинетическую энергию:

Q₁ Q₂,...... Q_n,

если только известна кинетическая энергия системы (7) в функции переменных:

q ₁, q ₂, q ₃...... q _n и их производных по времени, т. е. если известно соотношение:

Т =f{ q ₁, q ₂, q ₃ ,.....q_n, q' ₁, q' ₂, q '₃ ..... q' _n ).

Величины q называются обобщенными координатами. В качестве таковых могут быть выбраны, например, линейные расстояния (тогда система обобщенных координат в частном случае превра­щается в систему обыкновенных декартовых координат), углы (по­лучается полярная система, если второй координатой служит линей­ное расстояние), поверхности, объемы, а также вообще произвольные физические величины, имеющие характер протяженности или могу­щие характеризовать степень продвижения рассматриваемого кине­тического процесса. При этом обобщенная сила Q, действие которой проявляется в изменении соответствующей координаты q и сообщении некоторого приращения кинетической энергии системы Т, является физической величиной, имеющей характер напряженности. Произ­ведение обобщенной силы Q на приращение обобщенной координаты, D q должно выражать работу или энергию. Так, например, избрав в некотором случае в качестве обобщенной координаты количество воды, протекшей через поперечное сечение трубы, в качестве обобщенной силы мы должны избрать давление, ибо количество про­текшей воды надо помножить на соответствующее давление, чтобы получить работу. Такого рода соображениями необходимо руковод­ствоваться всегда при выборе обобщенных координат и сил, при­годных для описания некоторого кинетического процесса и опери­рования с лагранжевыми уравнениями второй формы.

Этот совершенно общий характер координат, входящих во вто­рую форму уравнений Лагранжа, особенно ценен для электро­динамики. Он позволяет нам обойти главное затруднение — наше неумение характеризовать электрокинетический процесс декартовыми координатами. Ниже мы будем говорить подробнее о выборе коор­динат для электродинамической системы, пока же отметим лишь, что именно эти „обобщенные" (название, установившееся позднее) координаты имеет в виду Максвелл в приведенном выше отрывке (§ 555), говоря о переменных.

Число обобщенных координат равно числу степеней свободы системы. Следовательно, если система имеет n степеней свободы, то число обобщенных координат будет также n:

q ₁, q ₂, q ₃....... q _n.

Производные обобщенных координат q по времени 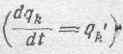называются обобщенными скоростями, так как всякая производная по времени, характеризуя быстроту изменения данной величины, имеет характер скорости.

Далее, для характеристики кинетического процесса, кроме коор­динат и скоростей, необходимо еще знание „сил", действующих в системе. В том общем методе, который мы сейчас рассматриваем, под „силой" понимается всякая причина изменения в кинетическом процессе. Все внешние „силы", действующие в системе, мы можем мыслить как ряд отдельных „сил" Q_k, соответствующих отдельным координатам q_k. Тогда величина координаты q_k и характер ее из­менения будут зависеть от подобной „силы* Q_k, которая и назы­вается обобщенной силой.

Как было выше указано, обобщенная сила Q_k есть величина, на которую надо умножить приращение, полученное координатой q_k, чтобы получить работу. И эта работа равна соответствующему приращению кинетической энергии системы.

Представление Максвелла о координатах как о величинах, определяющих положение некоторых ползунов, является примером того, насколько произволен может быть выбор обобщенных координат и сил. В этом примере величины, взятые в качестве обобщенных координат и сил, являются величинами совершенно фиктивными воображаемыми, которых реально в исследуемой системе нет. Однако, из этого не следует делать вывода,что обобщенными координатами или силами не могут являться реальные физические вели­чины, существующие в системе. (Понятие „обобщенный" не равно­сильно понятию „фиктивный").

Интересно теперь остановиться на ряде примеров, иллю­стрирующих характер обобщенных сил. Мы увидим, что обобщен­ная „сила", не всегда является силой в обычном элементар­ном смысле этого слова. Вспомним, что обобщенная сила должна удовлетворять только тому условию, что, будучи помножена на приращение надлежащим образом выбранной координаты, она должна давать работу.

Если обобщенной координатой служит количество воды, проте­кающей по трубе, то этому условию, как указано выше, удовле­творяет давление, расходуемое в данном участке трубы, т. е. да­вление будет являться обобщенной силой, хотя по размерности давление представляет собою обычную силу, деленную на площадь, Если обобщенной координатой служит угол поворота, то обобщен­ной силой будет вращающий момент (Ma =работе).

Выбирая в качестве обобщенной координаты поверхность, мы должны будем взять за обобщенную силу величину поверхностного натяжения.

Если обобщенной координатой служит объем (v), то за обобщен­ную силу следует взять давление (р), так как произведение давления на приращение объёма (p•dv) даёт работу.

Вернемся теперь к выражениям, являющимся второй формой уравнений Лагранжа:

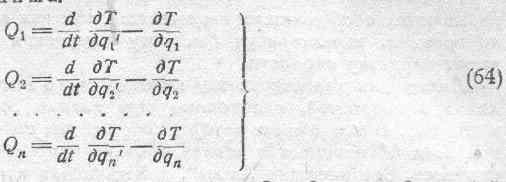
где Т— кинетическая энергия системы; Q ₁Q₂,... Q_n — обоб­щенные внешние силы; q ₁, q ₂ ,... q_n — обобщенные координаты; q '₁, q '₂,..... q '_n— обобщенные скорости.

Из данного выше определения обобщенных сил следует, что число уравнений (64) равно числу обобщенных координат и, ибо каждой обобщенной координате соответствует одна обобщенная сила.

Как указано выше, эти именно уравнения, ввиду их общности и сравнительной простоты, Максвелл и применил для изучения явлений электродинамики.

Вообще всегда, когда мы не умеем характеризовать процесс декартовыми координатами и не знаем ни характера, ни математи­ческого выражения связей системы, мы можем найти действующие в системе силы, пользуясь второй формой лагранжевых уравнений, Для применения этой последней нужно лишь уметь составить выра­жение кинетической энергии системы через обобщенные координаты и их производные по времени. Как мы увидим ниже, в случае электродинамической системы, выражение кинетической энергии получает сравнительно простой вид. Но сначала обратимся к выра­жению кинетической энергии в обобщенных координатах для про­извольной системы.

¹) См., например, И. В. Мещерский, „Теоретическая механика", ч. II.

²) Подробный вывод 2-й формы лагранжевых уравнений можно найти в III части курса проф. И. В. Мещерского „Теоретическая механика".

¹) В дальнейшем изложении из технических соображений будет приценяться обозначение q'.

²) В действительности мы будем дальше обозначать обобщенные силы через q,

Дата добавления: 2014-11-29