Энергия: пондеро-кинетическая, электрокинетическая и нондеро-электрокинетическая

По аналитическому строению выражения для кинетической энергии (Т) электродинамической системы можно судить и о фи­зическом характере этой энергии. В самом деле, выражение для кинетической энергии:

можно представить в следующем виде:

где:

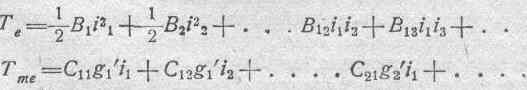
Первое слагаемое, Т'_m, зависит лишь от геометрических коор­динат и их скоростей. Если бы в рассматриваемой системе не существовало никаких электрических токов, то ее кинетическая энергия выражалась бы именно этим первым слагаемым. Таким образом, выражение Т_m, содержащее квадраты геометрических

скоростей и их произведения, представляет собою кинетическую энергию системы, рассматриваемой просто как система весомых масс.

Аналогично, второе слагаемое, Т_е, содержащее квадраты элек­трических скоростей (токов) и их попарные произведения, не зави­сит от геометрических скоростей. Т_е представляет собой кинети­ческую энергию системы, рассматриваемой исключительно как система электрических токов.

Наконец, последнее слагаемое, Т_me включает как геометриче­ские скорости, так и электрические токи.

Ввиду качественного различия этих трех слагаемых полной кинетической энергии системы, иногда присваивают каждому из, них особое наименование. Именно Т_m называют пондеро-кинетической энергией, т. е. энергией движения системы, рассматривае­мой как совокупность только весомых масс. При отсутствии в си­стеме электрических токов (i_k =0) кинетическая энергия ее вы­ражается лишь этою частью.

Т_е называется электрокинетической энергией. Это есть энергия системы, рассматриваемой как совокупность электрических токов, и зависящая исключительно от электрокинетических процессов.

Наконец, Т_me называется пондеро-электрокинетической энергией системы. Эта энергия может иметь конечное значение только при одновременном изменении и геометрических и электрических коор­динат. Возможность существования пондеро-электрокинетической энергии Т_me, как части полной кинетической энергии системы токов, была впервые установлена Максвеллом путем именно того ме­тода, изложению которого посвящены настоящие страницы. В то время как энергия T_m и энергия Т_е представляют собою физические ко­личества, по существу хорошо известные и в достаточной степени изученные в соответствующих областях науки, энергия Т_me яв­ляется до сих пор еще сравнительно мало изученной, и до Макс­велла она была совершено неизвестна.

¹) Термин „пондеро-кинетическая" происходит от латинского слова pondus (род. п. ponderis), обозначающего вес, и, таким образом, указывает на то, что

Дата добавления: 2014-11-29