Электродвижущая сила самоиндукции

Рассмотрим сначала простейшую систему, состоящую из одного проводящего контура (рис. 153).

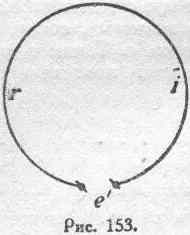
Если к этому контуру приложена внешняяэлектродвижущая сила e', то часть ее идет на преодоление омического сопротивления, а остаток — на изменение электрокинетической энергии си­стемы:

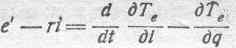
или, так как:

то:

Здесь мы имеем аналогию с механической системой, в которой обычно часть внешней приложенной силы идет на преодоление сопротивления среды. н лишь остаток расходуется на изменение кинетической энергии (живой силы).

Мы обозначили (см. § 97) величину дT_e/дi через p, поэтому мо­жем писать:

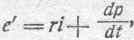
т. е. внешняя ЭДС идет на преодоление сопротивления и какой-то обратной, реактивной ЭДС. Эта обратная ЭДС (обозначим ее в этом случае через е_s) выразится так:

e_s=-dp/dt.

В случае чисто материальной простейшей динамической системы, состоящей из одной материальной точки, движущейся со ско­ростью v, электродвижущей силе e_s соответствует механическая сила:

откуда видно, что электродвижущая сила e_s имеет характер даламберовской силы инерции.

Электрокинетическая энергия одного контура выразится так:

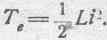
Следовательно, величина р, играющая роль количества движе­ния в электрокинетическом процессе, будет равна в данном случае:

а электродвижущую силу e_s получим, взяв от р производную по времени с обратным знаком, т. е.

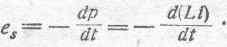
Таким образом, мы видим, что обратная ЭДС, могущая возникнуть в данной цепи в связи с изменениями электрокинетической энергии, будет зависеть от всяких изменений размеров и формы контура, а также от изменений силы тока. Ясно, что эта ЭДС есть не что иное, как открытая Фарадеем ЭДС индукции, называемая в данном случае электродвижущей силой индукции (e_s) ввиду того, что она индуктируется благодаря тем или иным изменениям, протекающим в самом рассматриваемом контуре.

На основании опытов Фарадея известно, что ЭДС индукции может возникнуть в контуре только при изменении величины магнит­ного потока, связанного с контуром, и равна скорости убывания потока, т. е.

Е=-dФ/dt.

Магнитный поток в рассматриваемом случае, очевидно, есть так называемый поток самоиндукции (Ф_s), т. е. поток, сцепляющийся с данным контуром только в силу того, что по нему идет ток; другими словами, это есть поток, являющийся неотъемлемой составной частью того электромагнитного процесса, который протекает в цепи. Таким образом, можем написать:

Отсюда

Интегрируя, получим:

Ф_e=Li +const.

Опыт показывает, что поток самоиндукции Ф_s может быть равен нулю только тогда, когда:

i =0.

Но в этом случае обязательно имеем:

Li =0.

Следовательно, постоянная интегрирования равна нулю, и мы получаем:

Ф_s=Li=р. (81)

Таким образом, величина р, играющая, как указано выше, роль количества движения в алектрокинетической системе, оказывается равной магнитному потоку, сцепленному с контуром. Это лишний раз подчеркивает уже неоднократно нами указанное основное по­ложение теории Максвелла, именно утверждение, что явления, про­текающие в магнитном поле, суть явления кинетического характера.

Коэффициент L, определяющий собою величину потока само­индукции при данной силе тока i, представляет собою фактор, от которого зависят все явления самоиндукции. Поэтому L называется коэффициентом самоиндукции..

Каждая электрическая цепь, совершенно независимо от того, входит ли она в состав сложной системы или рассматривается самостоятельно, обладает некоторым определенным коэффициентом самоиндукции, являющимся основной и весьма важной характери­стикой этой цепи в электромагнитном отношении.

Итак, электродвижущая сила самоиндукции в общем виде выра­жается так:

В случае', когда геометрические координаты данной системы неизменны, т. е. когда размеры и форма рассматриваемого контура остаются постоянными, очевидно мы будем иметь:

L=const.

В этом случае выражение ЭДС самоиндукции можно представить в следующем виде:

Наконец, могут быть случаи, когда тем или иным способом ток в цепи поддерживается строго неизменным, т. е. мы имеем:

i =const.

В этих случаях выражение ЭДС самоиндукции приводится

к следующей форме:

Дата добавления: 2014-11-29