Общее обследование сил, действующих в электродинами­ческой системе

При наличии в системе процессов механических и электриче­ских мы должны иметь в виду соответственно два рода сил: силы механические и силы электродвижущие. Если известна полная кинетическая энергия системы, то вторая форма уравнений Лагранжа дает возможность вычислить величины всех этих сил.

Остановимся сначала на механических силах. Если f'_k естьвнеш-

няя механическая сила, соответствующая координате g_k, то по уравнению Лагранжа, получаем:

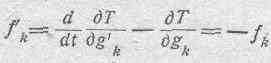
где f_k есть внутренняя реакция системы, имеющая природу даламберовской силы инерции. В дальнейшем мы нередко будем вместо внешних сил, воздействующих на данную систему и стремящихся изменить ее кинетическую энергию, рассматривать прямо противо­положные им силы реакции, являющиеся следствием существова­ния кинетической энергии в данной системе. Так как эти силы реакции равны по абсолютной величине и обратим по знаку внеш­ним силам, приложенным к системе, то ясно, что величины сил реакции просто получаются на основании лагранжевых уравнений. Рассмотрение именно этих, 'возникающих внутри системы, сил представляет интерес в том отношении, что в них проявляются наиболее характерные свойства системы.

Так как Т состоит из трех частей: Т =T_m+T_e+T_me, то при помощи теоремы о производной суммы мы можем разложить силу f_k на три составляющие, соответственно трем частям энергии:

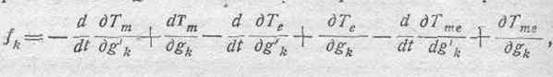
или же, обозначая три составляющие силы f_k через f_m, fe и f_me, а также опуская в дальнейшем ради простоты индекс „k", имеем:

где

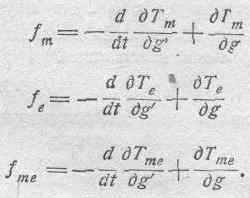
Рассмотрим все эти силы.

В выражение для механической силы:

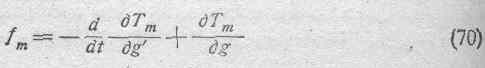
электрические координаты и их производные не входят. Это — та часть механической силы, которая возникает в системе в силу чисто механических условий и представляет собою обыкновенную даламберовскую силу инерции весомых масс. Изучение этих сил относится к области механики.

Обратимся к физическому смыслу второй составляющей, т. е.

силы f_e:

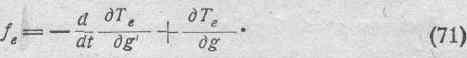
Так как величина электрокинетической энергии системы Т_е не зависит от геометрических скоростей g', то имеем:

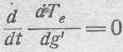
ивыражение для механической силы f_e принимает вид:

Эта сила представляет собою известную механическую силу электромагнитного происхождения, т. е. так называемую электро­магнитную силу. Так как она выражается однородной функцией вто­рой степени от всех токов системы, то она не меняет ни величины, ни направления, если изменить направление всех токов системы.

Наконец, составляющая механической силы, зависящая от воз­можного существования пондеро-электрокинетической энергии T_me,

т. е. сила:

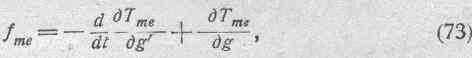
представляет собою проявление взаимодействия между движением электричества в проводнике и движением этого проводника, ана­логично тому, как имеет место зависимость между движением жид­кости и движением сосуда, в котором она находится.

Максвелл сделал попытку установить опытным путем нали­чие силы f_me. Выражение (73) показывает, что для обнаружения этой силы можно итти двумя путями, именно, обследовать порознь обе составляющие f_me, т.е. первый и второй члены в правой части соотношения (73).

Рассмотрим сначала систему, которая находится в покое, но токи в которой порознь не равны нулю. В этом частном случае пондеро-электрокинетическая энергия:

T_me=SC(g'•i)

равна нулю. Однако, соответствующая сила, величина которой определяется производными T_me, может быть и не равна нулю. Не трудно показать, что второй член в выражении силы f_me всегда равен в этом случае нулю, т. е.

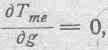
а первый член, вообще говоря, может быть не равен нулю, т. е.

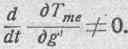
В самом деле, беря частную производную от T_me по геометри­ческой координате, мы получим выражение, равное нулю, так как в него входит множителем геометрическая скорость, равная в дан­ном случае нулю:

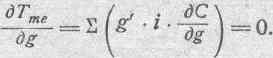
Что же касается первого члена, то, беря первую производную по геометрической скорости, мы исключаем из него g', вследствие чего, беря вторую производную по времени, мы получаем выра­жение, вообще говоря, не равное нулю:

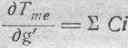
и

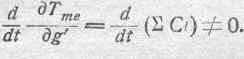
Отсюда видно, что выражение силы f_me в этом случае получает вид:

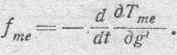
Итак, сила f_me будет положительна или отрицательна, смотря по тому, уменьшаются или увеличиваются в данный момент силы токов в соответствующих проводниках системы. Эта сила стано­вится равной нулю, как только силы токов в системе делаются

постоянными. Сверх того, так как дT_me / д g' представляет собою ли­нейную функцию от сил токов, то при данном изменении сил токов сила f_me изменяет свое направление в случае, если и все токи в системе делаются обратными по направлению.

В своем опыте, имеющем целью обнаружение механической силы f_те в рассмотренном случае, когда все частя системы нахо­дятся в покое, а силы токов изменяются, Максвелл применил про­стейшую систему, состоящую из одной только электрической цепи. Именно, он взял горизонтальную плоскую катушку, состоявшую из большого числа витков тонкой изолированной проволоки и имевшую прикрепленное к ней зеркальце. Катушка была подвешена центрально на тонкой проволоке, которая служила также для соеди­нения одного конца катушки с внешнею частью цепи. Другой конец катушки соединялся с тонкой проволочкой, опущенной в сосуд со ртутью и по своему расположению составлявшей

продолжение подвесной проволоки (см.рис. 151, на котором воспро­изведен оригинальный чертеж Максвелла).

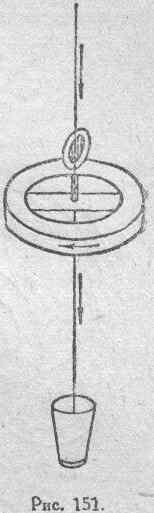
При помощи подвес­ной проволоки и проволоки, опущенной в ртуть, катушка вводилась в цепь батареи через особый замыкатель. Положение катушки можно было наблюдать посредством трубы и шкалы.

Так как мы имеем здесь лишь один электри­ческий контур, то его пондеро-электрокинетическая энергия выразится одним членом:

T_me=Cg'i,

откуда

а сила f_me, могущая проявиться в контуре, равна:

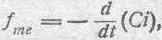
а потому при изменении силы тока в контуре, т. е. при замыкании и размыкании цепи, мы должны ожидать отклонения катушки под действием силы f_me. Однако, никаких отклонений обнару­жить не удалось. Таким образом, первый опыт Максвелла не дал положительного результата. Это не говорит, однако, о том, что пондеро-электрокииетическая энергия (T_me) не существует, а скорее о том, что величина ее, слишком мала и что экспериментальная обстановка, бывшая в распоряжении Максвелла, оказалась недоста­точной для обнаружения ее проявлений.

Максвелл обратился затем к обследованию той составляющей силы f_me, которая обусловливается наличием второго члена в пра­вой части соотношения (73). Если все токи в системе постоянны, но система находится в движении, этот второй член, вообще говоря, не равен нулю, т. е.

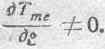
Соответственным образом может иметь некоторое конечное зна­чение и определяемая вторым членом составляющая силы f_me. При экспериментальном обследовании этого случая Максвелл остано­вился на

простейшей системе, состоящей из одной катушки с доста­точно большим числом витков изолированной проволоки. Для усиле­ния ожидаемого эффекта он поместил внутрь катушки железный сер­дечник. Построив специальный прибор, Максвелл пытался обна­ружить на опыте механическую силу, зависящую от существования электрического тока в катушке и некоторого, надлежащим образом выбранного, движения этой катушки. Максвелл остановился на вращательном движении катушки. На рисунке 152 воспроизведен оригинальный чертеж Максвелла, изображающий тот прибор, который был им применен в описываемом опыте. Электромагнит А имеет возможность вращаться вокруг горизонтальной оси ВВ' вну­три кольца, которое, в свою очередь, вращается вокруг вертикаль­ной оси. При помощи специальных винтов все подвижные части были надлежащим образом уравновешены для того, чтобы, по воз­можности, устранить при производстве опыта всякие вредные влияння и сделать систему весьма чув­ствительной только в отношении ожидаемых механических воздей­ствий со стороны обследуемой составляющей силы f_me. Большие затруднения возникали еще вслед­ствие действия земного магнитного поля, которое Максвелл до известной степени скомпенсировал при посредстве особого магнита. Проанализировав описываемую систему (рис. 152),

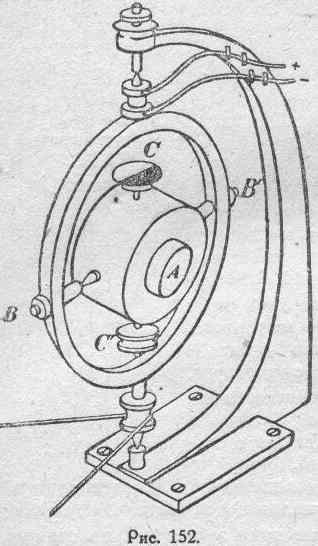
Максвелл пришел к заключению, что та ме­ханическая сила, которая в рас­сматриваемом случае может возни­кать вследствие одновременного существования вращения электро­магнита А вокруг вертикальной оси и постоянного электриче­ского тока, протекающего по его обмотке, будет стремиться повер­нуть электромагнит вокруг гори­зонтальной оси ВВ', совершенно аналогично тому, что получилось бы, если бы вместо электромагнита был взят, например, гироскоп или вообще какая-либо материальная масса, вращающаяся вокруг оси, совпадающей с осью железного стержня электромагнита. Ток в об­мотку электромагнита подводился через пружинные щетки, трущиеся о контактные кольца, закрепленные на вертикальном валу, и далее через подшипники В'. Вся система приводилась в быстрое враща­тельное движение при посредстве ремня, перекинутого через шкив на валу. За положением электромагнита можно было следить, не­смотря на быстрое вращение, благодаря следующему приспособле­нию. С телом электромагнита был жестко связан диск С, по диа­метру разделенный на две половины, соответственно окрашенные в красный и зеленый цвета. При горизонтальном расположении сердечника электромагнита (нормальное расположение) центр диска С совпадал с вертикальной осью вращения. В случае поворачивания электромагнита вокруг оси ВВ' в одну сторону, в средней части диска С, при быстром вращении всей системы, должен появляться

кружок, окрашенный, например, в красный цвет, при поворачивании же электромагнита в другую сторону — кружок, окрашенный в зеленый цвет. При этом диаметр окрашенного кружка будет определять угол поворота электромагнита вокруг оси ВВ'.

Результат, к которому пришел Максвелл при производстве описанного второго опыта, был также отрицателен: не удалось заметить никакого достоверного изменения в положении электро­магнита, быстро вращавшегося вокруг вертикальной оси, в то время как через его обмотку пропускался возможно более сильный постоян­ный ток. Должно при этом отметить, что сам Максвелл считал обстановку этого второго опыта в общем слишком грубой вслед­ствие того, что невозможно было вполне устранить целый ряд вредных влияний.

Рассмотрим теперь другую сторону проявлений кинетической энергии в электродинамической системе, т. е. в системе токов.

Если к некоторой части этой системы приложена внешняя ЭДС, равная e ₀, то за вычетом омического падения напряжения в соот­ветствующей цепи мы получим ЭДС, идущую на изменение кине­тической энергии системы. Обозначая эту последнюю ЭДС через е' можем написать:

e'=e₀-ri.

Так как е' есть сила, производящая изменение некоторой элек­трической координаты q, то зависимость силы е' от кинетической энергии системы выразится соотношением:

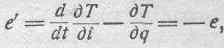
где е — внутренняя реакция системы (обратная ЭДС). Соответ­ственно трем составляющим кинетической энергии 'электродинами­ческой системы и ЭДС е. разобьется на три составляющие:

где,

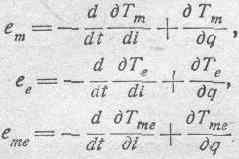
Но так как кинетическая энергия системы (Т) не зависит от электрических координат {q) (см. § 95),то все вторые члены правых частей этих уравнений равны нулю, т. е.

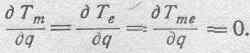
Поэтому выражения для обратной ЭДС примут следующий вид:

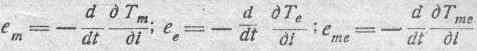
или

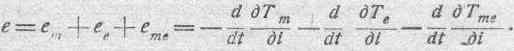
Пондеро-кинетическая энергия системы T_m не зависит от сил токов, существующих в системе, следовательно,

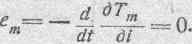
Электродвижущая сила е_е, равная взятой с обратным знаком производной по времени от частной производной электрокинетиче­ской энергии системы по соответствующей силе тока, представляет собою ЭДС индукции, открытую Фарадеем. Таким образом, выражение:

дает наиболее общее выражение для индуктированной ЭДС.

Подобное выражение для индуктированной ЭДС кажется несколько необычным; однако, легко показать, что оно не отличается принципиально от других, более известных нам выражении для ЭДС. В самом деле, как известно (ниже об этом говорится более подробно), выражение для электрокинетической энергии в простейшем, например, случае одного контура имеет вид:

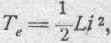
где L есть коэффициент самоиндукции контура. Беря в данном случае частную производную от T_e по силе тока, получим:

Но произведение Li есть не что иное, как некоторый магнитный поток Ф, связанный с контуром, т. е.

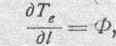
и мы приходим к знакомому уже нам выражению для ЭДС:

Этот пример показывает, что выражения (75) и (76) для ЭДС совпадают друг с другом и представляют собою два разные выра­жения одного физического закона.

Как видно из общего выражения:

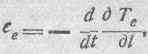
величина ЭДС, возникающей в системе, зависит от изменения сил токов, существующих в системе, от положения и формы проводников, составляющих систему, и от изменения их положения и формы. Действительно, выражение Т_е содержит коэффициенты, в которые входят геометрические координаты, квадраты сил токов и их произ­ведения. Следовательно, после двукратного дифференцирования (по i и по t) окончательное выражение для ЭДС будет содержать геометрические координаты, их производные по времени и произ­водные от сил токов по времени.

Наконец, третья составляющая электродвижущей силы:

так же, как рассмотренная выше механическая сила f_me, характе­ризует собою взаимоотношение между электричеством и материей. Электродвижущая сила е_me, как показывает вышеприведенное соотношение, зависит от скоростей и ускорений в движениях проводников и совершенно не зависит от токов в этих проводниках. Таким образом, если пондеро-электрокинетическая энергия (Т_me) действительно существует, то в данном проводнике должна, вообще говоря, возникнуть ЭДС при полном отсутствии электрических токов в системе, но при наличии ускорений или замедлений дви­жения системы. В частности, в случае подвешенной горизонтальной катушки, изображенной на рисунке 151, т. е. в простейшем случае одной цепи, мы будем иметь:

T_me=Cg'i,

где g' есть скорость вращения катушки вокруг оси подвеса. Отсюда получаем:

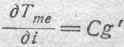
и далее:

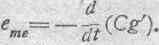
Если, следовательно, катушка находится сначала в покое, затем мы внезапно приведем ее во вращение вокруг вертикальной оси, то должна появиться ЭДС, зависящая or ускорения этого враща­тельного движения. При замедлении вращения и остановке должна

появляться ЭДС обратного знака. Максвелл и произвел такого рода опыт (третий опыт для обнаружения проявлений T_me). С этою целью катушка укреплялась на специальной оси, перпендикулярной плоскости витков катушки, и при помощи соответствующих гибких проводников приключалась к весьма чувствительному гальвано­метру. Максвелл сам в связи с этим отмечает:... „немногие научные наблюдения могут быть произведены с большею точностью, чем определение существования или несуществования тока, выпол­няемое при посредстве гальванометра. Чувствительность этого метода намного превосходит чувствительность большинства расположений, имеющих целью измерение механических сил, действующих на тело. Таким образом, если некоторые электрические токи могут быть возбуждены таким путем (т. е. сообщением вращательного ускоре­ния катушке), они были бы обнаружены, даже если бы они были весьма слабы". Производя опыт с вращательным ускорением катушки, Максвелл не заметил никаких признаков появления тока в цепи гальванометра. Тем не менее, такого рода ток, по существу, должен был бы появиться совершенно аналогично тому, как если бы вместо витков проволоки мы имели кольцевую трубчатую камеру, заполненную подвижною жидкостью. При вращательном ускорении кольцевой камеры вокруг оси симметрии, жидкость приобрела бы скорость относительно стенок трубчатой камеры, т. е. внутри этой камеры мы получили бы „ток жидкости".

Итак, все три опыта, поставленные Максвеллом для обнару­жения проявлений пондеро-электрокинетической энергии T_me дали отрицательный результат. На основании этого Максвелл заклю­чил, что если энергия T_me и существует как часть полной кинети­ческой энергии системы токов, то во всяком случае эта часть сравнительно столь мала, что проявлениями ее в обычных условиях мы можем пренебречь.

Принимая все это во внимание, мы будем, следовательно, в дальнейшем принимать:

T_me =0,

помня, вместе с тем, что это соотношение следует рассматривать все же не как точное выражение того, что в действительности имеет место, но лишь как практически допустимое приближение, значительно упрощающее изучение основных сил как механических, так и электродвижущих, могущих возникать в системе токов,

Теоретические соображения, приведшие Максвелла к пред­ставлению о пондеро-электрокинетической энергии (T_me), остаются в полной силе. После Максвелла другими исследователями возоб­новлены попытки обнаружить на опыте проявления энергии T_me. Работы этого рода приобрели особенный интерес за последнее время в связи с установлением того факта, что материя и элек­тричество по природе своей теснейшим образом связаны. Макс­велл несомненно предугадывал это, как видно из его слов, при­веденных в параграфе 91 настоящей главы (см. п. 569 в конце).

Современная теория строения вещества позволила произвести предвычисления величины тех сил механических и электродвижущих, которые могут возникнуть в системе в связи с существованием определенного соотношения между электричеством и материей, характеризуемого, между прочим, наличием пондеро-электрокинетической энергии T_me. Как и следовало ожидать, силы f_me и e_me столь малы, что даже при современных экспериментальных сред­ствах, значительно более совершенных, чем это было во времена, Максвелла) проявления этих сил лежат весьма близко к пределам чувствительности измерительных приборов и схем.

Эйнштейн и де-Гаас произвели опыт, который по существу вполне соответствует расположению первого опыта Максвелла, представленному на рисунке 151, и получили явно положительный ре­зультат, хотя и лежащий на пределе чувствительности метода. Отличие опыта Эйнштейна и де-Гааса от обстановки опыта Макс­велла заключается в том, что они вместо катушки, в которой воз­буждался ток от внешнего источника, воспользовались внутриатомны­ми токами в объеме железного стерженька, подвешенного вдоль своей оси на тонкой нити. Контуры внутриатомных токов, т. е. орбиты элек­тронов, нормально расположены в хаотическом беспорядке (см. § 37}. Если создать внешнее магнитное поле вдоль оси железного цилин­дрического стержня, например, замыканием тока в катушке, внутри которой расположен стержень, то возникает продольное намагни­чение его, обусловленное известным упорядочением в расположении электронных орбит: положительные направления их осей теперь ориентируются преимущественно в одном направлении вдоль оси стержня. Все происходит так, как будто бы в стержне возникли сильные токи, протекающие по виткам, перпендикулярным оси стержня или, что то же, линии подвеса. Изменяя направление тока в ка­тушке на противоположное, мы тем самым повернем в противо­положную сторону оси электронных орбит, т. е. вдвое увеличим тот эффект, который может быть обусловлен возникновением упо­рядоченных электронных токов в железном стержне. При про­изводстве опыта приходится очень бороться с мешающим механическим действием магнитного поля катушки, которое, при наличии трудно устранимой несимметрии в расположений железного цилиндра внутри катушки в связи с несимметричностью самого цилиндра, имеет результатом появление некоторого вращающего момента, маскирующего искомый эффект. Все же путем математической обра­ботки ряда наблюдений удалось констатировать наличие тех сил, обнаружение которых являлось целью первого опыта Максвелла.

Прямое отношение ко второму опыту Максвелла с прибором, представленным на рисунке 152, имеют исследования Барнетта, обстановка опытов которого заключалась в следующем. Железный стержень приводился в весьма быстрое вращательное движение и затем внезапно останавливался. Оказалось, что стержень намагни­чивался под влиянием вращения и затем во время остановки раз­магничивался. Это можно было обнаружить, окружив железный стержень катушкой с большим числом витков, присоединенной

к баллистическому гальванометру. Изменение магнитного состояния стержня проявлялось в возникновении индуктированного тока. В опыте Барнетта отдельные молекулярные магнитики в объеме железного стержня вели себя так, как должен был вести себя, согласно расчетам, электромагнит Л во втором опыте Максвелла (см. рис. 152). Отметим здесь же, что П. Н. Лебедев еще за­долго до опытов Барнетта пытался обнаружить намагничение вращающегося медного цилиндра.

Итак, анализ и экспериментальное обследование трех форм кинетической энергии электродинамической системы и сил, воз­никающих в этой системе, приводит к следующим заключениям.

Пондеро-кинетическая энергия T_m и обусловленные ею механи­ческие силы не связаны с электрическими процессами, происходящими в системе; эта часть энергии характеризует систему только как систему весомых масс, и изучение ее относится к области аналитической механики.

Пондеро-электрокинетическая энергия T_me и соответствующие

силы практически могут быть приняты равными нулю.

Электрокинетическая энергия T_e и соответствующие ей силы: электромагнитная (механическая) сила и электродвижущая сила индукции—являются результатом чисто электромагнитного про­цесса, происходящего в системе. С последними двумя силами при­ходится сталкиваться во всех областях электротехники, и изучение алектрокинетической энергии T_e и сил f_e и е_е представляется по­этому особенно существенным.

В заключение необходимо сделать еще одно замечание для устранения могущего возникнуть недоразумения. Напомним приня­тый нами порядок исследования, приведший к аналитическим выра­жениям f_e и е_е. Мы предполагали, что к системе приложена некоторая внешняя, в одном случае — механическая, в другом — электродви­жущая сила. Разлагая реакции, возникающие в системе под действием этих внешних сил, на составляющие, соответственно трем составляющим Т, мы и получили выражения для f_e и е_е:

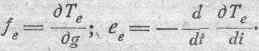
Из этих выражений видно, что механическую силу f_e можно

рассматривать не только как реакцию, возникающую в системе в ответ на приложенную внешнюю механическую же силу, но и как самодовлеющий результат чисто электромагнитного процесса а системе, как результат, обусловленный исключительно тем, что система обладает некоторой электрокинетической энергией. Точно так же электродвижущая сила e_e возникает в системе не только как реакция на приложенную извне электродвижущую силу, но и как самостоятельное явление, обусловленное всякими изменениями общих электромагнитных условий, которые имеют место в системе проводников.

Дата добавления: 2014-11-29