Координатах

Выражение для кинетической энергии в обобщенных

Переводчик.

Так как обобщенные координаты, как было выше указано, вполне определяют положение всех частей системы, то они должны быть связаны некоторыми зависимостями с декартовыми координатами всех точек системы. Следовательно, мы можем выразить декартовы координаты через обобщенные при помощи некоторых уравнений:

Всего таких уравнений будет 3 s, где s — число точек системы, заданных декартовыми координатами.

С другой стороны, из механики известно, что кинетическая энергия системы выражается в декартовых координатах так:

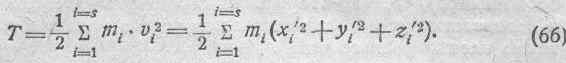
Чтобы получить выражение для кинетической энергии в обоб­щенных координатах, надо в выражение (66) подставить значения x '_i, y '_i, z '_i.Последние найдем, если возьмем производные по вре­мени от уравнений (65):

Возведя полученные выражения в квадрат, мы получим, во-первых, члены, содержащие квадраты обобщенных скоростей, а во-вторых, члены с их удвоенными произведениями.

Произведя подстановку и собирая члены с одинаковыми обоб­щенными скоростями, получим окончательно для кинетической энергии системы в обобщенных координатах:

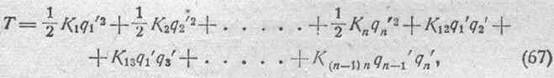
где коэффициенты К являются функциями обобщенных координат, но не их производных.

Таково выражение кинетической энергии всякой системы. В случае электродинамической системы, т. е. в случае системы токов, выражение для Т имеет тот же вид. Для составления этого выражения прежде всего обратимся к рассмотрению вопроса о вы­боре обобщенных координат для электродинамической системы.

Дата добавления: 2014-11-29