Коэффициент взаимной индукции

Совершенно подобно тому, что мы имели при определении коэффициента самоиндукции (см. соотношения 85 — 89 в § 99), и в случае количественного определения коэффициента взаимной индукции мы, вообще говоря, можем исходить из любого соотно-

шения, устанавливающего связь этого коэффициента с другими ве­личинами. Остановимся на простейших зависимостях этого рода:

При этом мы имеем в виду случай совершенно неизменяемой системы, состоящей из двух цепей, когда соблюдается условие:

m ₁₂= const.

Вместе с тем необходимо здесь же отметить, что в настоящем случае так же, как и при рассмотрении вопроса о коэффициенте самоиндукции, мы будем предполагать, что проводники с током находятся в пустоте. Рассмотрение же случая, когда пространство заполнено каким-либо веществом, например, железом, и когда мы по существу имеем дело с некоторым действующим коэффициен­том взаимной индукции, — отложим до параграфа 106, специ­ально посвященного вообще действующим коэффициентам индукции.

Отметим еще то обстоятельство, что в выражении для электро­кинетической энергии системы из двух цепей фигурирует только один коэффициент взаимной индукции, который мы обозначили через M ₁₂. С полным правом мы могли бы его представить и сим­волом M ₂₁. Одним словом:

M ₁₂ =M ₂₁,

т. е. коэффициент взаимной индукции между двумя цепями будет один и тот же, независимо от того, имеем ли мы дело с индуктив­ным действием первой цепи на вторую или второй на первую. Ввиду того, что в рассматриваемом случае двух цепей мы имеем дело лишь с одним вполне определенным коэффициентом взаимной индукции, можем обозначить его просто символом М без всяких значков. Таким образом, выражение для электрокинетической энергии в данном простейшем случае можно представить в следую­щей форме:

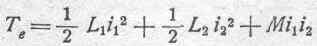
и вышеприведенные соотношения (95) перепишутся так:

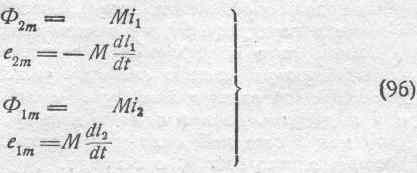
Пользуясь соотношениями (96), из выражений для магнитного потока взаимной индукции мы получаем:

т.е. коэффициент взаимной индукции, системы из двух цепей численно равен потоку взаимной индукции, сцепляющемуся с кон­туром одной из цепей, когда по другой цепи идет ток, сила ко­торого равна единице.

Выражая поток взаимной индукции и силу тока в абсолютных электромагнитных единицах, мы в этой же системе единиц выразим и коэффициент взаимной индукции. При этом:

М= 1, если имеем, например:

Ф_2т= 1 максвеллу

и

i ₁=1 абс. эл.-магн. единице.

Практическую электромагнитную единицу коэффициента взаим­ной индукции, называемую также генри, как и в случае самоиндукции, мы можем определить, исходя из выражений для электродвижущих сил в соотношениях (96). Именно отсюда мы получаем:

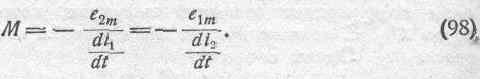
Полагая электродвижущую силу равною одному вольту и ско­рость изменения силы тока равною одному амперу в секунду, а также помня, что эти две величины всегда будут обратных зна­ков, получаем:

М= 1генри,

т. е. коэффициентом взаимной индукции в один генри обладает такая неизменяемая система из двух цепей, в одной из кото­рых, при неизменности тока в ней, индуктируется электродви­жущая сила в один вольт в то время, как в другой цепи сила тока равномерно изменяется со скоростью одного ампера в секунду.

Итак, генри есть вообще единица коэффициента индукции. Объ­единяя два определения генри, данные в настоящем параграфе и выше в параграфе 99, мы можем сказать:

Генри есть коэффициент электромагнитной индукции, ха­рактеризующий такую систему цепей; в одной из которых ин­дуктируется электродвижущая сила самоиндукции или взаим­ной индукции, равная одному вольту, в то время как в той же цепи или в соседней сила тока равномерно изменяется со ско­ростью одного ампера в секунду.

Все, что было сказано в параграфе 99 относительно полного магнитного потока самоиндукции, совершенно так же приложимо к случаю потока взаимной индукции. В данном случае, вообще го­воря, надо отличать полный поток взаимной индукции от реально существующего потока взаимной индукции. Первый есть не что иное, как полное число сцеплений реально существующего потока взаимной индукции с рассматриваемым сколь угодно сложным кон­туром. Умножая коэффициент взаимной индукции на соответствую­щий ток, мы получаем именно полный поток взаимной индукции, например:

Ф _2m =Mi ₁,

который будет равен реально существующему потоку лишь в про­стейшем частном случае, когда рассматриваемая (в данном случае — вторая) цепь состоит из одного лишь витка. В виде примера вычислим коэффициент взаимной индукции тороида достаточно малого сечения с двумя равномерно распределенными обмотками, соответственно состоящими из n ₁ и n ₂витков каждая (рис. 159).

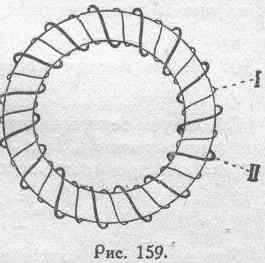
Для того, чтобы не осложнять вопроса (см. § 106), примем, что внутри тороида мы имеем дело с пустотой, для которой: m=m₀=1.

Допустим, что мы имеем предель­ный случай электромагнитной связи двух рассматриваемых цепей (обмоток), т.е. что магнитный поток, обусловливаемый током в одной из обмоток, например, в первичной, пол­ностью сцепляется со всеми без исключения витками вторичной обмотки. Другими словами, мы допускаем, что в данном случае отсутствует рассеяние магнитного потока.

Рассчитаем реально существующий магнитный поток Ф'. Если по первичной обмотке протекает ток, сила которого есть i ₁, то, обозначая площадь сечения тороида через s и, длину средней ли­нии через /, можем написать:

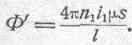
Полное число сцеплений этого потока со вторичной цепью, со­стоящею из n ₂витков, будет:

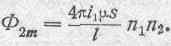
Величину коэффициента взаимной индукции М мы получим, разделив Ф _2mна i ₁:

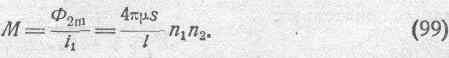
Так как в данном случае мы имеем дело с пустотой и потому

m=1,

то численному выражению для коэффициента взаимной индукции можно придать следующий вид:

Сравнивая выражения (99) и (100) с соответствующими выра­жениями для коэффициента самоиндукции тороида же (90) и (91), мы видим, что в обоих случаях мы имеем дело со второю степенью числа витков, причем при отсутствии магнитного рассеяния, как это именно и принято в обоих рассматриваемых случаях, коэффи­циент при второй степени числа витков остается один и тот же, независимо от того, имеем ли мы дело с квадратом числа витков (в случае L) или с произведением двух чисел витков (в случае М).

Дата добавления: 2014-11-29