Роль короткозамкнутой вторичной цепи

При рассмотрении явлений самоиндукции и взаимной индукции мы видели, что величина полной ЭДС, возникающей в некотором проводящем контуре в качестве реакции на производимое изменение общих электромагнитных условий, зависит не только от обстоя-

тельств, характеризующих данную цепь, но и от присутствия других цепей, не связанных электрически с данной:

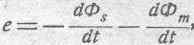
где Ф _s есть поток самоиндукции данного контура, а Ф_m — поток взаимной индукции, т. е. поток, обязанный своим существованием какому-нибудь внешнему для данного контура току (или токам). Чтобы лучше уяснить себе это влияние посторонних цепей, рассмотрим простейший случай двух цепей (рис. 161).

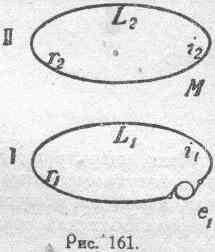
Пусть L ₁ и L ₂ — их коэффициенты самоиндукции, r ₁ и r ₂ — омические сопротивления, М-— коэффициент взаимной индукции. В одной из них (в первой) действует некоторая внешняя электродви­жущая e ₁в другой никакой внешней ЭДС нет. Для простоты возьмем случай, когда:

L ₁=const,

L ₂=const,

М =const.

Составим уравнение для тока в пер­вой цепи. Сила тока i ₁ в каждый дан­ный момент равна, согласно закону Ома, сумме действующих в контуре ЭДС, де­ленной на сопротивление, т. е.

или

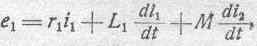
т. е. внешняя ЭДС преодолевает омическое сопротивление, обрат­ную ЭДС самоиндукции и ЭДС взаимоиндукции.

Для второго контура, в котором нет никакой внешней ЭДС, имеем аналогичное соотношение:

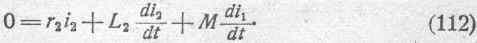
Исключим из уравнения (111) производную di ₂ /dt Для этого опре­делим ее величину из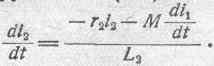

Подставляя в (111), получаем:

Сделаем еще одно допущение. Именно, положим, что:

r ₂=0,

т. е. представим себе, что во второй цепи мы имеем дело со сверх­проводником. Это в значительной степени упрощает окончательный вывод и позволяет легче разобраться в физическом смысле полу­ченного соотношения, характеризующего общие электромагнитные ' условия. Тогда из последнего уравнения получаем:

или, вводя обозначение:

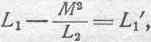
имеем:

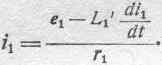
Итак, выражение для тока в первой цепи при наличии второй цепи, электромагнитно связанной с первой, мы привели к такому виду, какой мы получили бы, если бы второй цепи совсем не было, а первая обладала коэффициентом самоиндукции:

Таким образом, величину L' ₁мы можем рассматривать в каче­стве некоторого действующего коэффициента самоиндукции пер­вичной цепи, пользуясь которым мы как бы игнорируем наличие вторичной цепи и ведем расчет так, как будто бы существует только одна первичная цепь сама по себе. При этом, на основании данного выше соотношения М £ Ö (L ₁ L ₂ ), ясно, что, в зависимости от величины коэффициента связи k, будем иметь то или иное значение L '₁.

Если коэффициент связи k равен единице, т. е. М= Ö (L ₁ L ₂ ), то получаем идеальный случай:

L '₁=0,

другими словами, электромагнитная инерция рассматриваемой (пер­вой) цепи как бы совершенно уничтожается действием коротко замкнутой вторичной сверхпроводящей цепи.

Если коэффициент связи k равен нулю, т. е. M= 0, то имеем:

l' ₁ =l _i,

другими словами, в этом случае присутствие вторичной цепи не оказывает никакого влияния на электромагнитный процесс, про­исходящий в первичной цепи.

При всех значениях коэффициента связи, больших нуля и меньших единицы, значение действующего коэффициента самоиндукции L' ₁ будет больше нуля и меньше L ₁, т. е.:

0 <l' ₁ <l _i.

Таким образом, хотя истинный коэффициент самоиндукции ка­ждого контура и является функцией только его геометрических раз­меров, но в случае системы из нескольких электромагнитно свя­занных между собою контуров, каждый из них ведет себя по отношению к внешней ЭДС как контур, обладающий коэффициен­том самоиндукции L', величина которого для простейшего случая двух цепей определяется данным выше соотношением и может быть изменена путем изменения коэффициента связи k. Это именно и позволяет нам назвать величину:

действующим (эквивалентным, эффективным) коэффициентом само­индукции.

Если r ₂¹0, сущность явления не меняется, лишь математическое его выражение получается сложнее.

Обратимся к физическому смыслу рассмотренного явления, т. е. кажущегося уменьшения коэффициента самоиндукции контура вследствие присутствия вблизи него другого замкнутого проводящего контура. Дело в том, что возникновение в первом контуре тока i ₁ под действием приложенной к нему внешней электродвижущей силы е ₁вызывает возникновение во втором контуре тока i ₂, вообще говоря, обратного направления, так как магнитный поток Ф ₁, на­растающий вокруг первого контура, пересекает второй контур. Вторичному току i ₂ соответствует вторичный поток Ф_II, направле­ние которого обратно направлению потока Ф_I. Таким образом, по­ток Ф_II полностью или частично (в зависимости от степени связи) компенсирует действие потока Ф _I. В результате, реально суще­ствующий поток, сцепленный с первым контуром, оказывается меньше, чем при отсутствии вторичного контура. Следовательно, меньше будет и обратная ЭДС, индуктируемая в первом контуре, т. е. этот контур будет оказывать меньшее противодействие уста­новлению в нем тока. Иными словами, электромагнитная инерция контура становится меньше.

Все изложенное относится к категории явлений, охватываемых обобщенным законом Ленца, о котором мы уже говорили в главе I (см. § 29). Закон этот гласит, что всякая электромагнитная система стремится сохранить неизменным связанный с ней магнитный поток (количество движения). Именно такое стремление обнаруживается и в данном случае: на установление внешним воздействием (внеш­ней ЭДС) потока в первом контуре система реагирует созданием обратно направленного магнитного потока, обусловленного наличием второго проводящего контура.

Дата добавления: 2014-11-29