Электромагнитная сила. Общие соображения

При анализе связи между кинетической энергией, присущей элек­тродинамической системе, и силами, возникающими в такой системе, было получено (см, § 96) общее выражение для так называемой электромагнитной силы, т. е. механической силы, возникающей

в системе вследствие происходящих в ней электромагнитных про­цессов.

Это общее выражение (72):

определяет электромагнитную силу как частную производную от электрокинетической энергии системы по геометрической координате.

В дальнейшей необходимо неукоснительно помнить, что при об­следовании электродинамических систем при помощи второй формы лагранжевых уравнений мы принимаем в качестве независимых координат — количества электричества q и геометрические коорди­наты g, определяющие размеры, форму и взаимное расположение всех частей системы. В связи с этим мы, следовательно, должны считать, с одной стороны количества электричества и их производ­ные по времени, т. е. силы токов, независимыми от геометриче­ских координат, и с другой стороны, геометрические координаты независимыми от каких бы то ни было обстоятельств, характеризу­ющих систему с точки зрения электромагнитных процессов, в ней протекающих.

На основании изложенного, всякий раз, когда мы берем произ­водную электрокинетической энергии по геометрической коорди­нате, необходимо принимать все точки в системе постоянными.

Для того, чтобы возможно лучше охватить содержание выше­приведенного выражения (72), удобно представить его в виде отно­шения частных дифференциалов:

Таким образом, электромагнитная сила, стремящаяся изменить некоторую геометрическую координату, численно равна прираще­нию электрокинетической энергии, соответствующему приращению этой координаты на единицу, при условии, что токи поддержи­ваются постоянными.

Если, при условии постоянства токов в системе, электромагнит­ные силы совершают положительную механическую работу, то одно­временно получается положительное приращение электрокинетической энергии. На это обстоятельство обратил в свое время внима­ние В. Томсон (Кельвин). Действительно, если под действием силы f_e некоторая часть системы получила в направлении этой силы перемещение dg, то совершенная при этом работа dA будет поло­жительна и равна произведению силы на перемещение:

dА = f _е dg

или, так как

то

другими словами, положительной работе dA, совершаемой возникшей в системе электромагнитной силой, соответствует положительное же приращение электрокинетической энергии, по величине равное dA, при условии, что токи поддерживаются постоянными.

Отсюда непосредственно вытекает следующее весьма важное положение: во всякой электродинамической системе, силы токов в которой поддерживаются постоянными от каких-либо посто­ронних источников, возникают такие и только такие механи­ческие силы, которые приводят к увеличению электрокинетиче­ской энергии системы в результате вызываемых ими движений. Иногда этот закон формулируется короче: всякая электродинами­ческая система, в которой силы токов поддерживаются посто­янными, стремится увеличить свою электрокинетическую энергию.

Основываясь на вышерассмотренных рассуждениях, приведших к соотношению (120), В. Томсон указал, что если в рассматри­ваемом случае система черпает энергию от постороннего источника, то последний должен доставить системе количество энергии dA', равное двойной величине произведенной в системе работы или удво­енному приращению электрокинетической энергии системы:

dA'=dA+d_gT_e=2dA=2d_gT_e.

Отсюда, между прочим, следует, что всякий электромагнитный механизм, питаемый постоянным током, без особых дополнитель­ных приспособлений (напр., коммутаторов) может превратить в механическую работу не более половины получаемой им от внешнего источника электрической энергии, т. е не может иметь коэффици­ента полезного действия выше 50%. С рассматриваемой точки зрения необходимо признать, что коммутатор двигателя постоянного тока, сверх обычно учитываемых его функций, играет еще особо важную роль в энергетическом отношении. Именно, в процессе комму­тации в течение того промежутка времени, когда некоторая секция коротко замкнута через щетку, за счет запаса электрокинетической энергии, соответствующей этой секции, совершается некоторая меха­ническая работа до тех пор, пока сила тока в короткозамкнутой секции не сделается равной нулю. Эта механическая работа присо­единяется к той работе, которая совершается за счет энергии посто­янного тока, возбуждаемого в цепи двигателя непосредственно от генератора. Благодаря такому полезному превращению энергии, не­прерывно накопляемой в отдельных секциях обмотки якоря, когда они находятся вне зоны коммутации, результирующий коэффициент полезного действия электродвигателя постоянного тока может воз­растать и практически возрастает значительно выше 50%.

Сформулированный выше общий закон движений во всякой электродинамической системе, в которой сохраняются неизменными силы токов, а именно, положение о стремлении системы к увели­чению ее электрокинетической энергии, в этом случае можно выра­зить еще иначе. Для этого обратимся к электрокинетической энер­гии в общем случае:

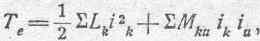
или, так как l_k i_k = Ф '_kесть поток самоиндукции k -ого контура,

а поток взаимной индукции между контурами k и u, то можем написать:

Отсюда видно, что если силы токов в составляющих систему контурах поддерживаются постоянными при помощи внешних источ­ников энергии, то приращение электрокинетической энергии может выразиться только суммой членов вида:

¹/₂idФ_s и idФ_m,

где Ф_s есть некоторый поток самоиндукции, а Ф_m — поток взаимной индукции. На основании соотношения (120) ясно, что этою же сум­мой выразится, вообще говоря, и работа каждой из электромагнит­ных сил, действующих в системе. При этом члены вида:

¹/₂idФ_s

обусловливаются изменениями коэффициентов самоиндукции и, соот­ветственно, потоков самоиндукции, а члены вида:

idФ_m

обусловливаются изменениями коэффициентов взаимной индукции и, соответственно, потоков взаимной индукции, т. е. так называемых внешних потоков, сцепляющихся с каждым данным контуром.

Отсюда следует, что работа электромагнитной силы положительна, когда положительно приращение потока, что дает для закона дви­жений в электродинамической системе такую формулировку: в элек­тродинамической системе стремятся возникнуть такие движения, в результате которых поток, связанный с каждым из составляю­щих систему контуров, мог бы получить положительное прира­щение в случае постоянства всех токов.

В случае жестких, неизменяемых контуров, т. е. когда все коэф­фициенты самоиндукции сохраняют свое значение, каждая из элек­тромагнитных сил f_e, действующих в системе, может совершить работу dA только в связи с изменениями потоков взаимной индук-

ции Ф_m (внешних потоков) и потому имеет место следующее соот­ношение:

dA=f_edg=idФ_m, (121)

справедливое в отношении каждого отдельного контура.

Отсюда вытекает простой способ для определения величины электромагнитной силы, действующей на тот или иной неизменяе­мый контур. Действительно, из соотношения (121) следует:

т. е. электромагнитная сила численно равна произведению силы тока в неизменяемом контуре на приращение сцепляющегося с ним внешнего магнитного потока, соответствующее прираще­нию геометрической координаты на единицу, при условии, что ток поддерживается постоянным.

Если, следовательно, в данной системе некоторый постоянный ток протекает по неизменяемому (L =const) контуру, сцепляющемуся с внешним потоком, то этот контур стремится двигаться таким образом, чтобы охватить наибольший внешний поток.

Если этот внешний поток обусловливается током в определен­ном втором контуре, причем токи в рассматриваемых двух конту­рах одинаково направлены, то стремление к увеличению охватыва­емого внешнего потока выражается в стремлении к увеличению коэффициента взаимной индукции M.

Единичный контур, по которому течет постоянный ток и который находится в собственном магнитном поле, стремится увеличить потек самоиндукции, что ведет к увеличению коэффи­циента самоиндукции L. Но этот коэффициент является, как нам уже известно, функцией геометрических координат, т. е. размеров и конфигурации контура. В случае контура, кривизна которого во всех его частях одного знака, увеличение L сопровождается увели­чением площади контура. Поэтому в этом частном случае можно говорить, что контур под действием электромагнитной силы стре­мится увеличить охватываемую им площадь. Подробнее об этом будем говорить ниже.

Уже из всего вышесказанного следует, что приведенные форму­лировки закона, которому подчиняется движение во всякой электро­динамической системе, не независимы одна от другой, а являются различными выражениями некоторого основного, единого в своей сущности, физического свойства магнитного поля. Чтобы выяснить

эту основу возникающих в электродинамической системе сил и дви­жений, уяснить взаимную связь приведенных выше формулировок и точнее установить, в каких случаях и как каждая из этих форму­лировок применима, обратимся к более детальному рассмотрению вопроса о физической природе электромагнитной силы с точки зре­ния фарадеевских представлений, касающихся магнитного поля, а также с точки зрения энергетических соотношений в системе.

Дата добавления: 2014-11-29